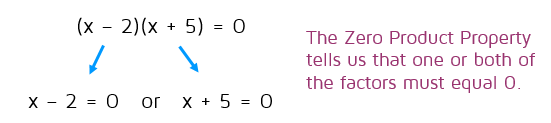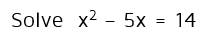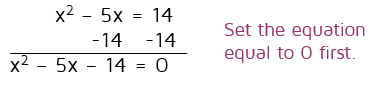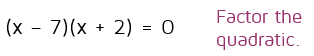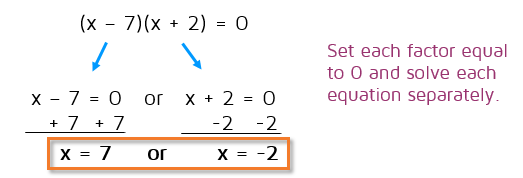Accompanying Resources: 
​Study Guide, Fun Activity, Google Drive Activity

​The Zero Product Property

Let's say I have two mystery numbers and I've written them on cards that I'm holding behind my back.  I tell you that if I multiply the two numbers together, the answer I get is 0.  What does this tell you about the numbers I wrote down?

The only way for two numbers to multiply to 0 is for one, or both, of them to be 0.  One of the numbers I wrote down must be 0 in order for them to multiply to 0.  Or maybe both of the numbers I wrote down were 0.  

​The Zero Product Property says that if two numbers a and b have a product of 0, then one or both of them is equal to 0.

The Zero Product Property is especially helpful for solving quadratic equations.  If you can set the equation equal to 0 and factor it, you'll be able to use this property to solve it.  Open the next tab to see how.

Solving Quadratic Equations by Factoring

Let's start by looking at a quadratic equation that's already been factored:  (x - 2)(x + 5) = 0
The two factors are x - 2 and x + 5.  We know that their product is 0 - when we multiply them together they equal 0.  We know from the Zero Product Property that this means one or both of them must be 0. This means that we can split the equation up into two separate equations.

In this example, the two separate equations are pretty easy to solve.  You can solve each one separately to find the two possible solutions.

Welcome to Kate's Math Lessons!  

Teachers: make sure to check out the study guides and activities.

Not all quadratic equations look the same as the example we just had. If you're going to solve a quadratic equation with this method, the first thing you need to do is make sure the equation is set equal to 0. You can't use the Zero Product Property if it's not set equal to 0.  If your equation isn't set equal to 0, just move everything over to one side to get it set equal to 0.

​Example 1

The first step is to set the equation equal to 0.  We can do this by subtracting 14 from both sides.

Now that it's set equal to 0, we need to factor it.  We need two numbers that multiply to -14 and the middle terms need to add up to -5x.  This means we want (x + 7) and (x - 2).  If you  need help factoring, make sure to check out the lesson on factoring quadratics.

Now we can use the Zero Product Property.  We have two factors that multiply to 0.  The Zero Product Property tells us that one of those factors, or both, must equal 0.  Now all we need to do is to split it up and set each factor equal to 0 and solve for x.

Example 2

If you're having trouble with the factoring step, make sure to try out the practice problems from the factoring quadratics lesson.

Alternatives to Factoring

Unfortunately, you won't be able to solve every quadratic equation with this method.   If you end up with a quadratic expression that can't be factored, you'll need to solve it a different way.  If this happens, you can solve it by using a method called completing the square, or by using the quadratic formula.  Click on the links below to learn more about these alternative methods to solving quadratic equations.

Introduction to Completing the Square
The Quadratic Formula

Practice

Ready to try a few problems on your own? Click the START button below to try a practice quiz.

Powered by