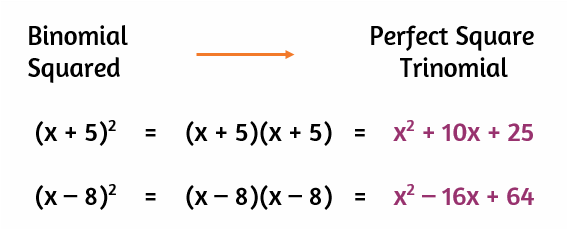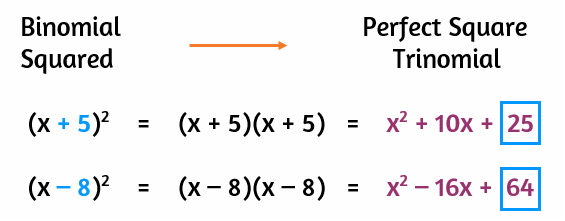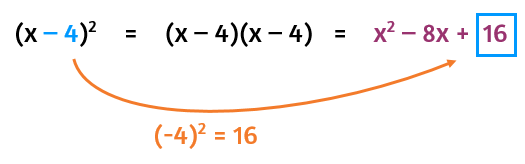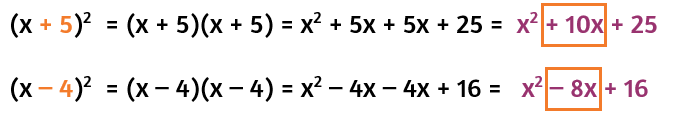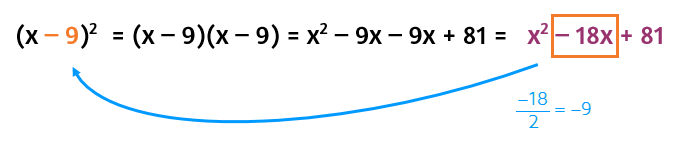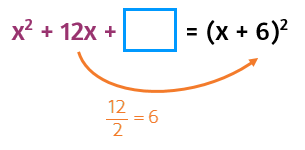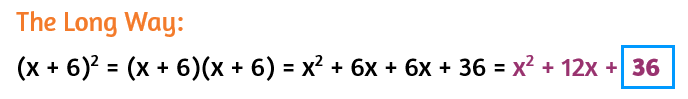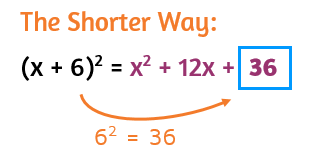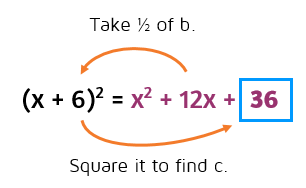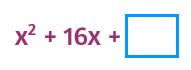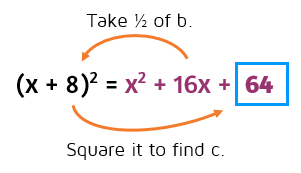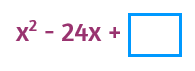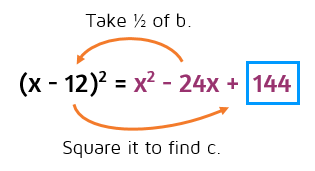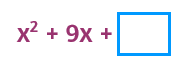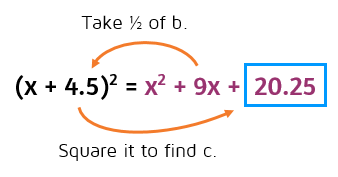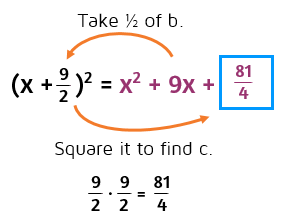|
|
When you use FOIL to simplify the multiplication, the constant at the end comes from the numbers in the "Lasts" spots. Since we're squaring a binomial, the numbers in these spots are the same. In the first example above, the 25 at the end came from multiplying the two 5's by each other. The 64 came from multiplying -8 by itself. If you square the second term of the binomial, you get the constant term of the perfect square trinomial.
Did you also notice that the constant at the end is always positive? Any time you square a number, the product will be positive. A perfect square trinomial will always have a plus sign before the last term.
Next, take a look at the middle term of the perfect square trinomial. How is it related to the original binomial that's being squared?
In the first example, the 10x came from the two 5x's being added together. In the second example, the -8x came from the sum of the -4x's. In both of these cases, half of the coefficient of the middle term is equal to the second term of the binomial.
Anytime the first term of the binomial is just an x, the second term of the binomial is half of the coefficient of the middle term of the perfect square trinomial.
Important Note: This does not apply if the first term has a coefficent other than 1.
Completing the Square
Completing the square is somewhat like factoring. When you factor a trinomial, you have to work your way backwards to figure out what to put in two sets of parentheses. When you're completing the square, you're trying to think backwards to "fix" an expression and make it into a perfect square trinomial.
Start by looking at the coefficient of the middle term: the 12. In order to end up with a 12x in a perfect square, you'll need to have two 6's in the original binomial. You can divide the coefficient of the middle term by 2 to figure out what goes in the parentheses.
Once you've figured out what goes in the binomial, you can find the constant that will be at the end of the perfect square trinomial. The long way is to write the binomial out twice to square it and use FOIL to simplify.
The shorter way is to use the shortcut and remember that the constant is always equal to the square of the second term of the binomial.
Here's a summary of the shortcuts we found to form a perfect square trinomial:
When you take 1/2 of b, it gives you the second term of the binomial in parentheses. Then square this number to find the constant that you need to make a perfect square trinomial.
Example 1
Complete the square.
To complete the square, first take half of b. This gives you the number that goes in the parentheses. Then square it to find c.
Half of 16 is 8. 8 squared is 64.
Example 2
Complete the square.
First take half of b. Then square it to find c. Half of -24 is -12. -12 squared is 144. Notice that it is positive. A negative times a negative is always positive. The constant at the end of a perfect square will always be positive.
Example 3
Complete the square.
This one's a little trickier because it has an odd number for b. We still follow the same process. Half of 9 is 4.5, 4.5 squared is 20.25. When b is an odd number, you'll have a decimal or fraction for c.
Answer as a decimal:
You may be asked to keep the answer as a fraction. If so, you can leave half of 9 as the fraction 9/2. Then multiply 9/2 by itself. Remember, multiply straight across when multiplying fractions.
Answer left as a fraction:
Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.
|
Powered by Interact |
Ready to see how you can solve a quadratic equation by completing the square?