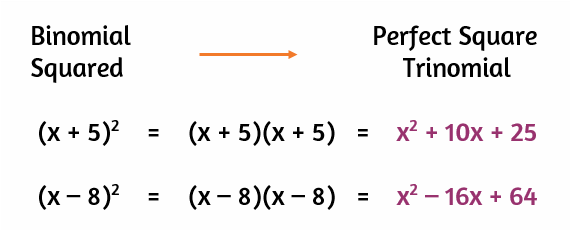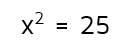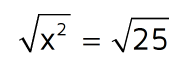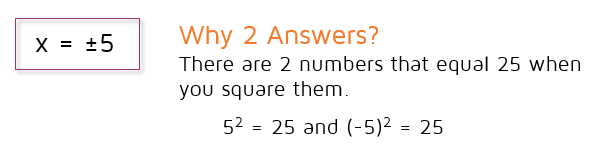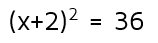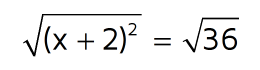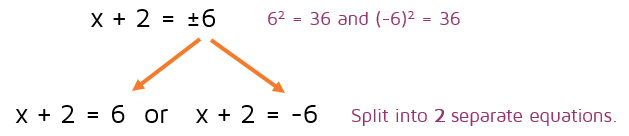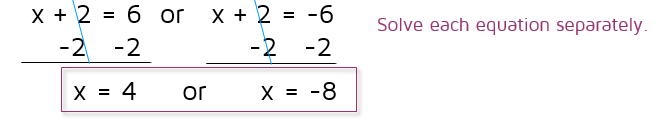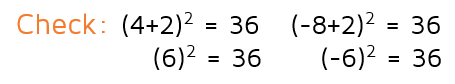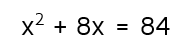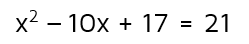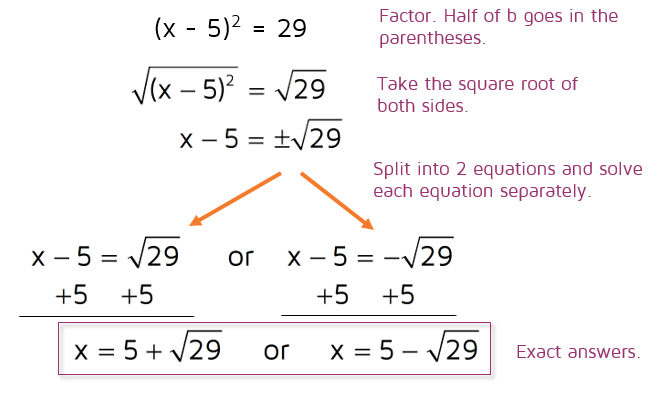Accompanying Resource: 
​Printable Study Guide

​

New to completing the square? You may want to check out the intro lesson before continuing.

Perfect Square Trinomials

When you square a binomial, the product is called a perfect square trinomial. You can distribute twice (FOIL) to multiply the two binomials together.  The simplified answer is the perfect square trinomial.

​Solving Equations with Perfect Squares

Before we look at equations with perfect square trinomials, let's start with a more basic equation with a perfect square.

In this problem, we need to figure out what x can be so that when we square it, it comes out to 25.  To undo squaring, we can use the inverse operation and take the square root of both sides.

Here comes the tricky part.  If you use a calculator and plug in the square root of 25, it will tell you the answer is 5.  This is correct, 5 squared does equal 25.  That's not the only answer though.  -5 squared also equals 25 (a negative times a negative is equal to a positive).  A calculator will only give you the positive answer when you use the square root button.  When you take the square root of both sides, you have to remember that there are usually two solutions.  You can write out the answer as x = 5 or x = -5.  You can also write the answer using the plus or minus sign.

Welcome to Kate's Math Lessons!  

Teachers: make sure to check out the study guides and activities.

Now let's look at an equation with a perfect square trinomial that's already been factored.  

We need to use inverse operations to work our way backwards and get x by itself.  In this equation, they added 2 first and then squared that number. If we go backwards, we need to undo the squaring first.  We can do this by taking the square root of both sides.

Remember, this is where you need to be careful.  If you hit the square root button on your calculator, it will tell you the answer is positive 6.  You need to remember that there are two numbers that equal 36 when you square them: 6 and -6.  This means that x + 2 could be equal to 6 or -6.

Since there are 2 possible solutions, we need to split it up into 2 separate equations.  x + 2 could equal 6 or -6.  This gives us two equations we can solve separately.

It's not too much work to check your answers.  We can plug in 4 and -8 back into the original equation and make sure they both come out to 36 to check our answer.

​Completing the Square

If this is new to you, make sure to check out our intro to completing the square lesson. Sometimes you will need to "fix" a trinomial to make it a perfect square. In this lesson, we're going to stick with perfect squares that have a 1 for the leading coefficient.  Here's the shortcut to figuring out what the constant needs to be at the end to make a perfect square trinomial: 

Let's look at an equation that does NOT have a perfect square:

The first step is to "fix" the expression on the left and make it into a perfect square.  We can figure out what we want c to be by taking half of 8 and squaring it.  Half of 8 is 4, 4 squared is 16.  (Check out the intro to completing the square lesson if you need help with this step.) This means we want a 16 at the end on the left side of the equation.  We do this by adding 16 to both sides of the equation. A common mistake is to only add it to one side. Make sure to keep things balanced by doing the same thing on both sides of an equation.

Now that you've "completed the square" by creating a perfect square trinomial, you can factor the left side. You can use educated guess-and-check to factor it, but it's faster to use the shortcut that we discovered in the intro lesson.  The number in the parentheses will always be half of b.

Once you get to this step, the problem is just like the one we did earlier.  Take the square root of both sides, remember there will be 2 answers (unless it's set equal to 0).  Split into two separate equations and solve each one separately.

Example 

Solve for x by completing the square.

​This equation does not have a perfect square.  You cannot factor the left side as it is currently.  This means we need to "fix" it first before we can move on.  There's more than one way to do this, but we think the easiest first step is to move the 17 out of the way.  We can do this by subtracting 17 from both sides.  This will give us an equation similar to the last one we did.

Next, figure out what you want c to be so that you can create a perfect square trinomial on the left side of the equation.  Take half of b and square it.  Half of -10 is -5.  -5 squared is a positive 25.  We can now create a perfect square trinomial by adding 25 to both sides.

Now you've "completed the square" by creating a perfect square trinomial on the left side.  The next step is to factor it.  Remember, you can use the shortcut to factor it.  Half of b will always be the number inside the parentheses.  Once you've factored it, take the square root of both sides.  Set up two separate equations and solve them separately.

These are the exact answers.  Depending on what number you end up with under the square root, you may have to simplify a radical before you write the exact answer.  In this case, the square root of 29 cannot be simplified.  If you're asked to give a rounded answer, you can plug the answers above into a calculator and round to get an approximate answer.

​Practice

Ready to try a few problems on your own? Click the START button below to try a practice quiz.

Powered by Interact

​Want to see another way to solve a quadratic equation?
​Check out the Quadratic Formula lesson.