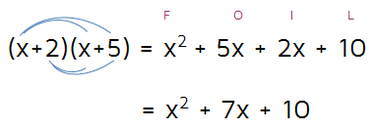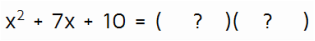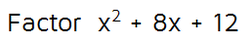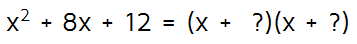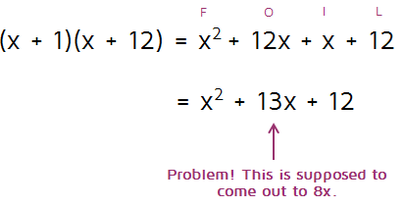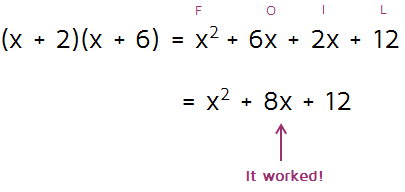|
Factoring Quadratics (Level 1: leading coefficient = 1) Page 1 of 3 Accompanying Resources: Task Cards, Boom Cards Fun Group Activity, Google Drive Activity
|
|
In order to factor this, we need to figure out what the two binomials are that multiply to the quadratic we've been given.
We need to know ( ? ) times ( ? ) will equal this quadratic expression. We know that the x-squared term will come from multiplying the Firsts - this means that there must be an x in both Firsts spots. We also have all plus signs in the quadratic, so the two binomials will also have plus signs. This gives us:
Now we just need to figure out what goes in the Lasts spots. We know that we have to end up with a 12 at the end of the quadratic for this to work. This means that the Lasts have to multiply to 12. Thankfully, there's only a few combinations of numbers that multiply to 12.
Options for Lasts spots:
1 and 12
2 and 6
3 and 4
Now we can just pick a combination and try it to see if it works. Let's try the 1 and 12 first. Distribute twice (FOIL) to see if it comes out to the quadratic we've been given.
Options for Lasts spots:
1 and 12
2 and 6
3 and 4
Now we can just pick a combination and try it to see if it works. Let's try the 1 and 12 first. Distribute twice (FOIL) to see if it comes out to the quadratic we've been given.
So this combination didn't work. The quadratic we were given has an 8x in the middle and this combination gave us 13x. Since this one didn't work, cross it off and try the next option: 2 and 6.
We found the two binomials that correctly multiply to the quadratic we were given. This means the final answer is (x+2)(x+6).
The good thing about factoring is that you can always check your answer. You can use what you know about the distributive property (FOIL) and narrow it down to only a few different possible options. Pick an option and use FOIL to see if it works. If it doesn't, cross it off and move on to the next one. The more you do these, the easier they will get.
The good thing about factoring is that you can always check your answer. You can use what you know about the distributive property (FOIL) and narrow it down to only a few different possible options. Pick an option and use FOIL to see if it works. If it doesn't, cross it off and move on to the next one. The more you do these, the easier they will get.