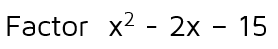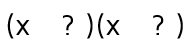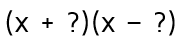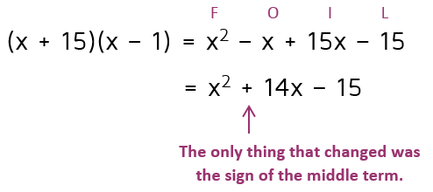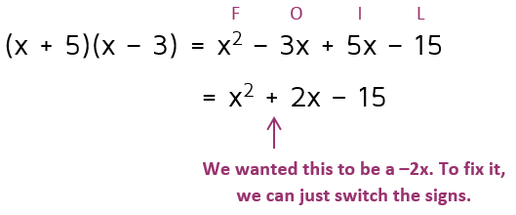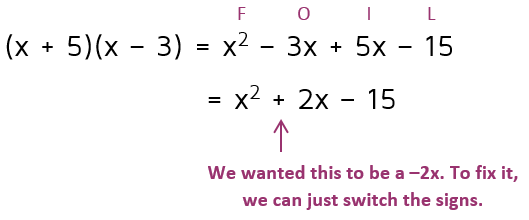|
Factoring Quadratics (Level 1) Page 2 of 3
Example 2The goal is to figure out ( ? ) times ( ? ) equals the quadratic we've been given. We know if we distribute (FOIL), the first term has to come out to the x-squared. This means we'll need an x in both the Firsts spots. This gives us: The constant at the end of our quadratic is a -15. This means the two numbers in the Lasts spots must multiply to -15. How do you get two numbers to multiply to a negative? One of them must be positive and the other one must be negative. A common mistake that students make on this type of problem is that they see two negatives in the quadratic and assume that the factored answer will have two negatives. If you multiply a negative by a negative, you'll get a positive at the end. Anytime the last number in the quadratic is negative, you'll need one plus sign and one minus sign. This gives us: |
|
Now we need to think about the possible numbers for the Lasts spots. We know they need to multiply to -15 and that one will be positive and the other will be negative. When you write out the options, don't worry about the signs. We can fix that at the end if we need to.
Options for Lasts spots:
1 and 15 (with either the 1 or the 15 negative)
3 and 5 (with either the 3 or the 5 negative)
How do we know which option it is? Just pick one and try it. Let's try the 1 and the 15 first. Don't stress out about which one to make negative. Just try it and see if it works.
So this option didn't work. Let's see if it works if we switch them and make the 1 negative this time.
Any time you just switch the two signs, the only difference in the answer will be that the middle term will change signs. Knowing this fact can save you a lot of time when you're trying to find the factors. Let's say you wanted the middle term to be 10x and you got a -10x. To fix the problem, all you do is switch the signs.
Now that we've ruled out the 1 and the 15 as an option, let's try the 3 and the 5. Remember, don't worry about which one to make negative. If we get a positive 2x in the middle instead of a -2x, all we need to do to fix it is to switch the + and - signs.
Once we switch it to a positive 3 and a negative 5, it works!
This means the final answer is (x+5)(x-3). The more you practice factoring, the easier it will get. You may even start to be able to eliminate certain possibilities in your head if you can recognize ahead of time that the middle number is going to end up too large or too small.