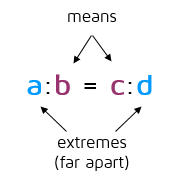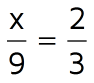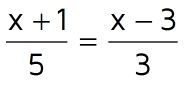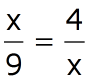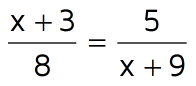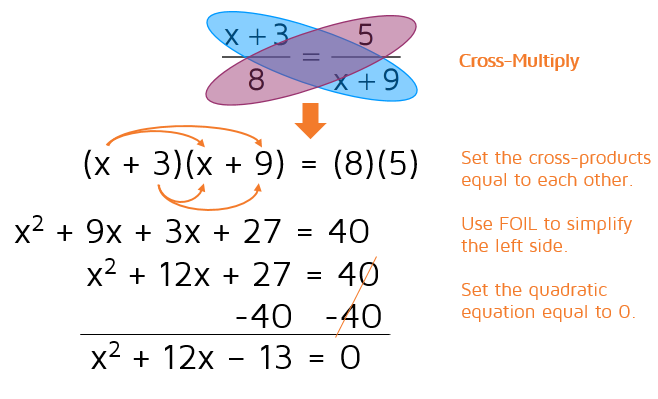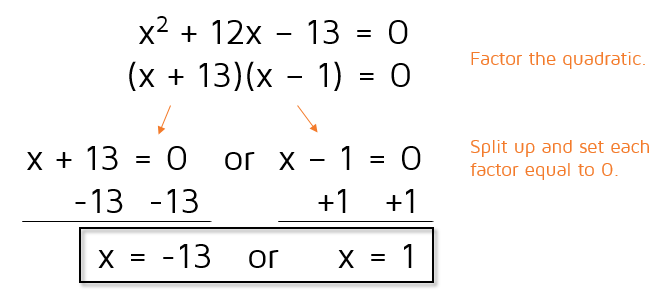|
Accompanying Resources: Proportions Google Activity, Printable Study Guide, Proportions Boom Cards (digital task cards), Ratio and Proportions Mazes
What is a Proportion?There are a few different ways to define a proportion. One way to describe a proportion is that it's an equation with two equal ratios. In other words, a proportion is when you have two fractions with an equals sign in the middle. Some proportions just have two fractions set equal to each other. Proportions can also have variables in one or both of the fractions. This lesson will show you how to solve for a variable that's in a proportion.
|
|
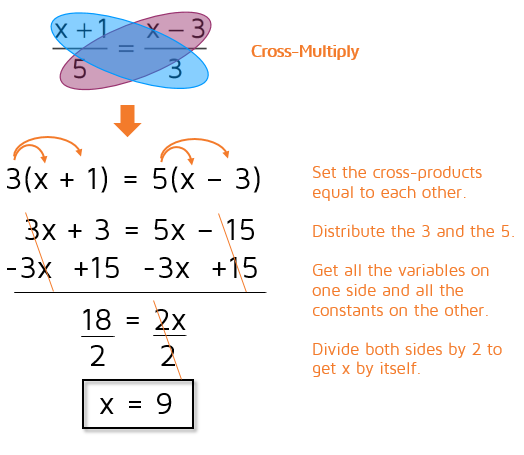
Why is this called the Means Extremes Property? The proportion can also be written with colons as a:b = c:d. The extremes are the terms that are furthest apart on the outside: the a and the d. The means are the terms on the inside: the b and c. This property says the product of the means is equal to the product of the extremes: ad = bc.
If you have a variable in your proportion, you can cross-multiply and get an equation that is much easier to solve.
Example 1
Solve for x.
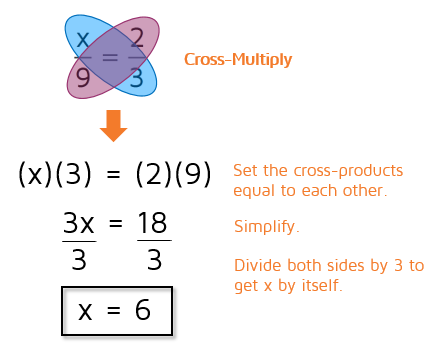
There's more than one way to solve this proportion. To solve it by cross-multiplying, you multiply diagonally and set the two cross-products equal to each other. Multiply the x and the 3 together and set it equal to what you get when you multiply the 2 and the 9 together.
|
A common mistake that students make when they cross-multiply is that they forget about the equals sign and write the two parts as a new fraction. Make sure to always put the equals sign in between the two cross-products. If you're solving an equation and your equals sign has disappeared, you have a problem! Example 2Solve for x.
First, cross-multiply. Be extra careful when you simplify each side. Make sure to distribute the 5 and the 3. If the middle steps didn't make sense to you, you make want to check out the lesson on solving equations with variables on both sides for a refresher. The next two examples are a little bit harder to solve. Example 3Solve for x.
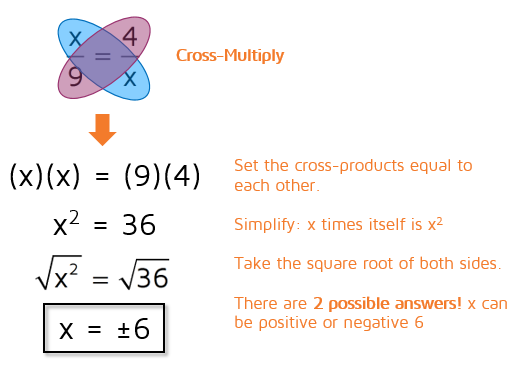
In this example, you end up multiplying x by itself when you cross-multiply. x times another x is x-squared. You can undo squaring the x by taking the square root of both sides. Be extra careful if you end up with an x-squared term when you cross-multiply. This is a quadratic equation and quadratics often have 2 solutions. In this case, we're looking for a number that equals 36 when we square it. We can take the square root of both sides, but we need to remember that a calculator will only give the positive solution. 6 squared equals 36, but -6 times -6 also equals a positive 36. You can find similar equations in the lesson on completing the square if you have more questions on this step. Example 4Solve for x.
In this problem, you have to multiply x + 3 by x + 9 when you cross-multiply. When you multiply two binomials by each other (x + 3 and x + 9 are called binomials because they have 2 terms), you need to distribute twice - this is often called the FOIL method. Make sure to check out the lesson on multiplying binomials if you need help with this step. When we cross-multiplied, we ended up with a quadratic equation (it has an x-squared term). There are several different ways to solve quadratic equations. You can complete the square, use the Quadratic Formula, or solve by factoring. It's usually fastest to try and factor if you can, so we recommend always trying to factor first. In this case, the quadratic we have on the left side can be factored. Once you have it factored, set each factor equal to 0 and solve. Make sure to check out the lesson on solving quadratic equations by factoring if you need more help with this type of problem. PracticeReady to try solving a proportion on your own? Take the practice quiz below:
|
|