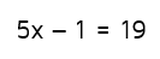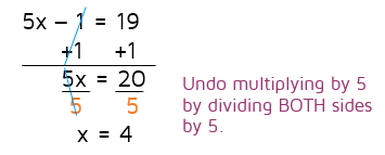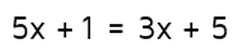|
Solving Equations with Variables on Both Sides Page 1 of 4 Accompanying Resources: Study Guide, Google Drive Activity, Fun Activity, Boom Cards, Assessment Review of Two-Step EquationsIn order to understand the equations in this lesson, it's important that you understand how to solve one-step equations and two-step equations. Equations with variables on both sides involve a few more steps, so I want to make sure you understand the simpler equations first before moving forward. Let's say you have the equation below:
This equation means that if you multiply a "mystery number" x by 5 and then subtract 1, the answer will be 19. To solve for x, you need to work your way backwards to get x by itself. Since the subtraction was done last, that's the first thing that needs to be undone. How do you cancel out subtracting 1? You need to use the inverse operation and add 1 to both sides. Remember to always do the same thing on BOTH sides of the equation to keep things balanced. Remember to use inverse operations to work your backwards and get x by itself. Undo addition and subtraction before you undo multiplication and division. Now we're left with the equation 5x = 20. This means that when you multiply x by 5, you get 20. How do you undo multiplying by 5? You use the inverse operation and divide both sides by 5. |
|
Once you have your answer, it's a good idea to check it to make sure it's correct. To check our answer, we can just plug in 4 for x in the original equation and make sure it comes out to 19.
Solving Equations with Variables
on Both Sides
Sometimes you'll get an equation that's a little more complicated than the one above. If you're in an algebra class, you'll likely run into an equation like this:
Example 1
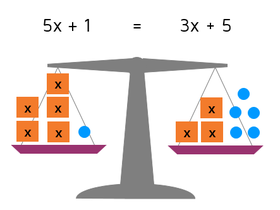
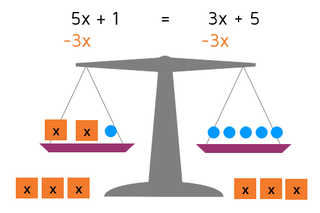
What's the big difference between this equation and the one we solved earlier? This equation has variables on both sides of the equals signs. Remember, you can visualize an equation using a balance scale. We could use the picture below to represent the equation:
On the left, there are 5 boxes with x in them. On the right, there are 3 boxes with x in them. Remember, if we do anything to the equation we have to make sure that we do the same thing to both sides to keep it balanced. Even though we don't know what x is, we know that each box containing x weighs the same amount. If we take 3 of the boxes off each side, it will still be balanced because each box weighs the same.
Anytime you have an equation with variables on both sides, it's a good idea to try to cancel them out on one side. The goal is to get all the variables on the same side - this will give you a simpler equation to solve. You can add or subtract terms with variables in them, just like you add or subtract numbers on each side.
In this equation, you can move all the variables to the left side of the equals sign by subtracting 3x from both sides.
Open the next page to see what to do next.