|
Scale Factors of Similar Figures Page 1 of 3
Accompanying Resources: Study Guide, Activity, Task Cards/Boom Cards What are Similar Figures?Similar figures are figures that have the same shape. They can be the same exact size, or one can be larger than the other.
The symbol for "is similar to" is a little squiggly line (called a tilde). 
When two shapes are similar, their corresponding angles will be the same. The angles are the same because the shape is still the same. You can tell from the order of the similarity statement which angles match up. In the example, angles A and D are the same (both letters are in written first), angles B and E are the same (both letters are written in the middle), and C and F are the same (both letters are written last). 
|
|
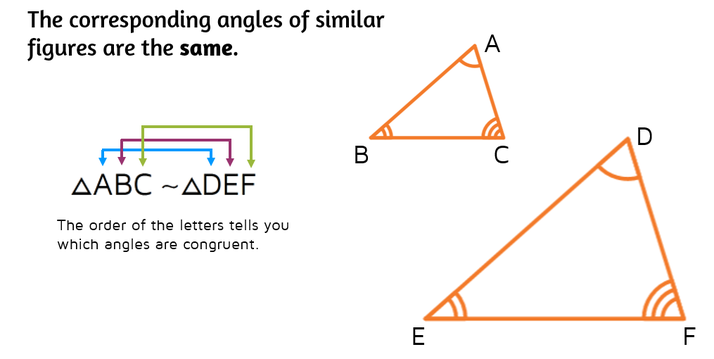
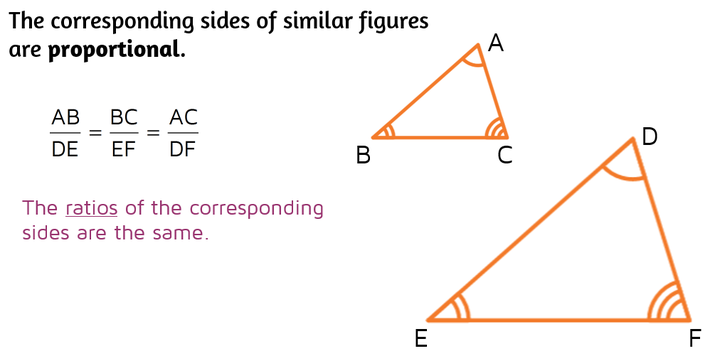
Similar triangles can be different sizes, so the lengths of the corresponding sides are not necessarily the same, but they are proportional. This means that the ratios of the corresponding sides are equal.
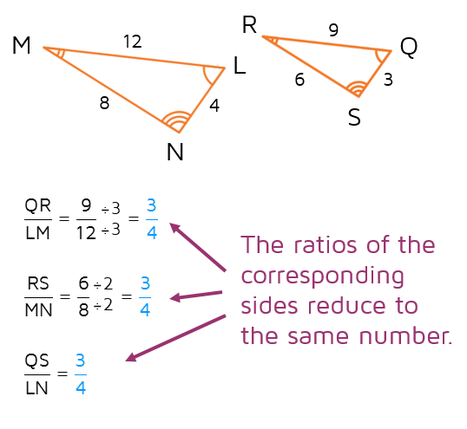
This might be easier to understand with an example. If we divide all the corresponding sides (in the same order), we see that each ratio came out to 3/4. When two shapes are similar, the ratios of the corresponding sides will be the same. In other words, the side lengths are proportional. Not sure what a proportion is? Check out the lesson on proportions.
What is a Scale Factor?
The ratio that you get when you divide corresponding side lengths of similar figures is called the scale factor. In the last example, the ratios all simplified to 3/4 so we would say that the scale factor of triangle LMN to triangle QRS is 3/4.
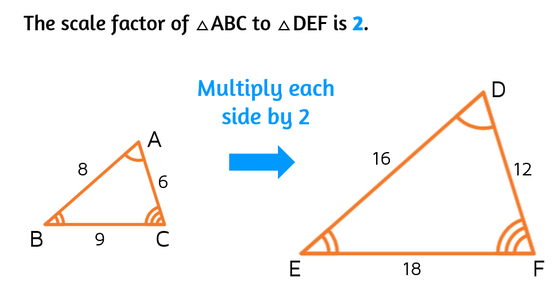
Another way to describe a scale factor is that it's a multiplier. In the example below, the scale factor of triangle ABC to triangle DEF is 2. This means that the second triangle is 2 times as big. If you multiply a side from triangle ABC by 2, you get the length of the corresponding side of triangle DEF. You can also get 2 as the scale factor by finding the ratios: 12/6 = 2, 16/8 = 2, and 18/9 = 2. The ratios of the corresponding sides are all equal to 2.
Another way to describe a scale factor is that it's a multiplier. In the example below, the scale factor of triangle ABC to triangle DEF is 2. This means that the second triangle is 2 times as big. If you multiply a side from triangle ABC by 2, you get the length of the corresponding side of triangle DEF. You can also get 2 as the scale factor by finding the ratios: 12/6 = 2, 16/8 = 2, and 18/9 = 2. The ratios of the corresponding sides are all equal to 2.
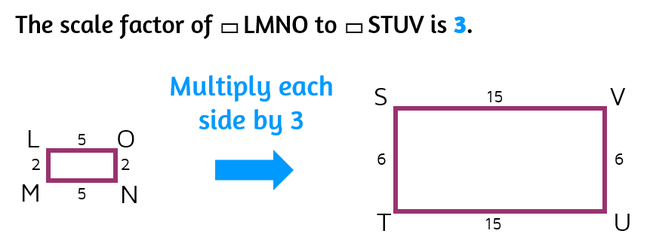
Here's another example. The scale factor of rectangle LMNO to rectangle STUV is 3. That means that the second rectangle is 3 times as big as the first rectangle. If you multiply the length of a side of the first rectangle by 3, you get the length of the corresponding side of the second rectangle.
You can also find the scale factor for the rectangles above by finding the ratios. 15/5 = 3 and 6/2 = 3. If you can't figure out what the side of the first shape is being multiplied by, you can go backwards and divide to find the scale factor.
