|
Scale Factors of Similar Figures Page 2 of 3
Does the Order Matter?Yes. The order is very important when you write a scale factor. If the scale factor of shape #1 to shape #2 is 4, that means the second shape is 4 times as big. If you look at the ratios, 20/5 = 4 and 16/4 = 4.
|
|
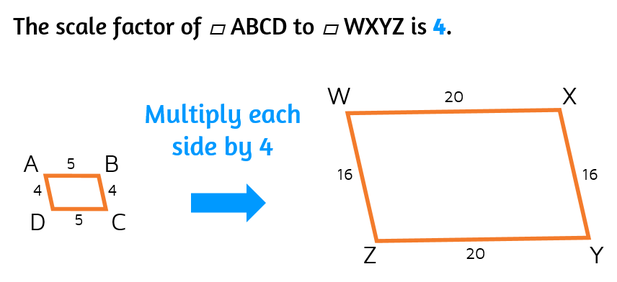
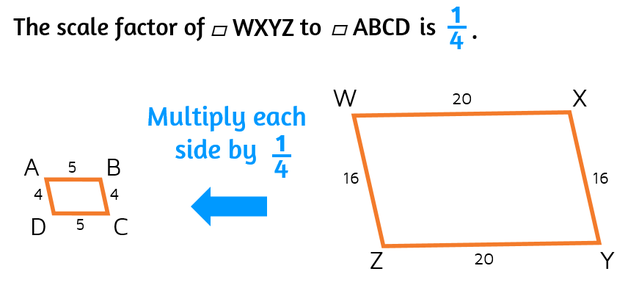
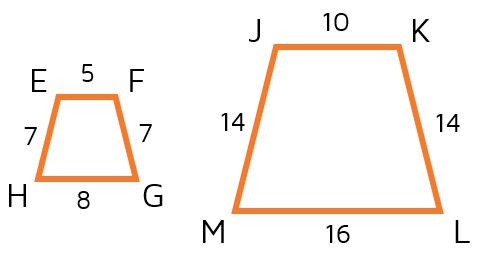But what happens if we switch the order? We wouldn't want to say that the scale factor is still 4 if the second shape is smaller. Remember, the scale factor is a multiplier. What can we multiply by if the second shape is smaller?
If you know the scale factor when the second shape is bigger, the scale factor of the other way around will be its reciprocal (flip the fraction upside down). This happens because the ratios will all be switched around. In the example above, we 20/5 and 16/4 to get the scale factor when the second shape was larger. If we switch the order, the ratios become 5/20 and 4/16, which both reduce to 1/4.
Pay close attention to the order of the two shapes. The first shape listed is what you start with. If the second shape is larger, the scale factor will be greater than 1. If the second shape is smaller, the scale factor will be smaller than 1.
Assume all shapes in the examples below are similar. Pay careful attention to the order of the shapes when finding the scale factor.
Example 1
Find the scale factor of trapezoid EFGH to trapezoid JKLM.
Notice that the smaller shape was listed first. If the second shape is larger, that means the scale factor will be larger than 1. What can you multiply a side of the first trapezoid by to get the length of the corresponding side on the larger trapezoid? If you multiply each side of the first trapezoid by 2, you get the lengths of the sides from the larger trapezoid. This means the scale factor is 2. You can also see that it's two by finding the ratios: 14/7 = 2, 10/5 = 2, 16/8 = 2.
|
|