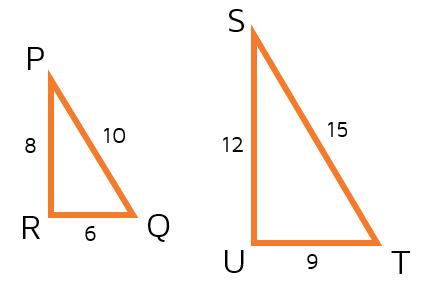Scale Factors of Similar Figures                       Page 3 of 3

Example 2

Find the scale factor of triangle PQR to triangle STU.

 
The second triangle listed is larger than the first, so we know that the scale factor is going to be larger than 1.  This time, the scale factor is not a whole number so it's not as easy to tell what it is.  It's not twice as big or three times as big.  If you can't tell right away what the scale factor is, you can find the ratios of the corresponding sides.  Make sure to go in the right order.  We know the scale factor will be larger than 1, so we need to put the larger number in the numerator of the fraction.  This gives us the ratios 12/8, 15/10, and 9/6.  These all reduce to the fraction 3/2, or 1 1/2 (the second triangle is a little less than twice as big).  We usually leave the scale factor as a fraction, so we would say that the scale factor is 3/2.    

Example 3

Find the scale factor of triangle STU to triangle PQR.

Did you notice the only difference between this problem and Example 2?  The order has been switched around.  Since the second triangle listed is smaller, the scale factor this time should be smaller than 1.  We already know the scale factor going the other way around, so we can just find its reciprocal (flip the fraction over).  If we did the ratios this time, they would all be switched around and have the smaller numbers on top: 8/12, 10/15, 6/9.  These all reduce to 2/3.  

Practice

Click the START button below to try some problems on your own.

Powered by

         1      2      3