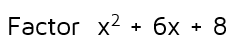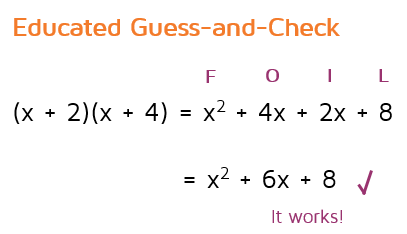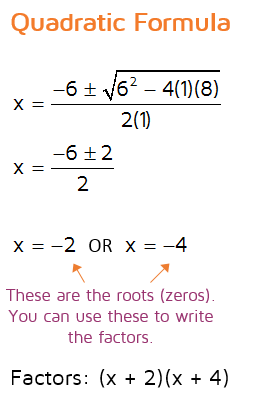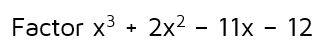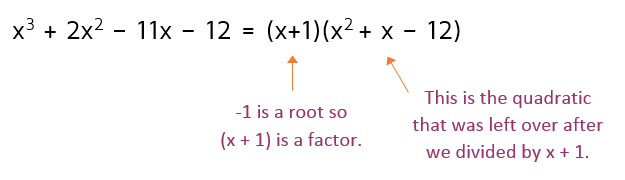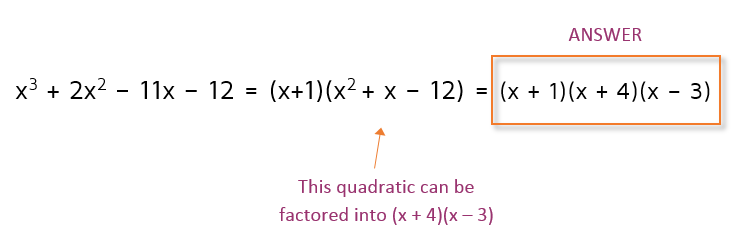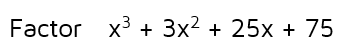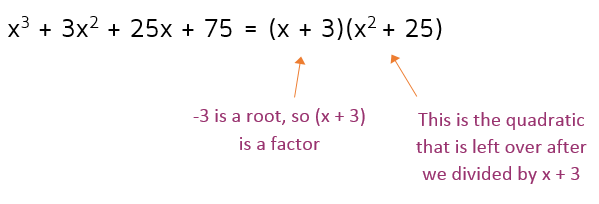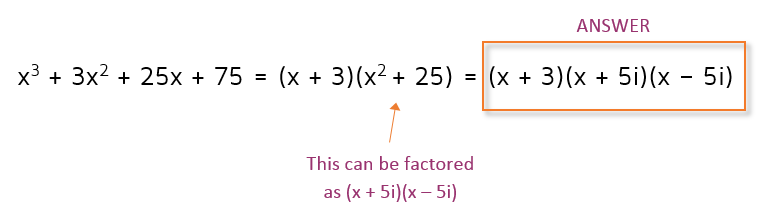|
Accompanying Resource: Printable Study Guide Factoring QuadraticsThere are a few different ways you can factor a quadratic expression (check out a lesson on factoring if this isn't familiar to you). You can use educated guess-and-check and use FOIL to see if you've factored it correctly. Let's say we have to factor the quadratic below:
We could use educated guess-and-check to factor this quadratic. We know that the numbers in the LAST spots must multiply to 8. This means we could try 1 and 8 or 2 and 4. In order to end up with a 6x in the middle, we need to use the 2 and the 4. You could also use the Quadratic Formula to find the roots of the quadratic. We need to plug in 1 for a, 6 for b and 8 for c. We can see that it simplifies to -2 and -4. Remember, the Quadratic Formula gives you the roots (zeros). These are the values that make the expression equal to 0. We can use the roots to write the factors. If -2 is a root, that means (x +2) is a factor. If you plug -2 into (x + 2), it equals 0. Likewise, if -4 is a root, that means (x + 4) is a factor. |
|
Factoring Higher Degree Polynomials
If the polynomial is degree 3 or higher, you can't use the Quadratic Formula. You could try educated guess-and-check, but it might take all day. Sometimes the factors involve irrational or imaginary numbers, so it would be near impossible to find them by guessing. There actually is a Cubic Formula you could use for 3rd degree polynomials, but it's quite complicated to use.
So are we just out of luck? Thankfully no. There's a Rational Roots Theorem that says if a polynomial has a rational root, it can be written in the form p/q where p is a factor of the constant term and q is a factor of the leading coefficient. It doesn't tell you what the roots are, but it at least helps you narrow down options to try.
Let's say you have to factor the polynomial below:
So are we just out of luck? Thankfully no. There's a Rational Roots Theorem that says if a polynomial has a rational root, it can be written in the form p/q where p is a factor of the constant term and q is a factor of the leading coefficient. It doesn't tell you what the roots are, but it at least helps you narrow down options to try.
Let's say you have to factor the polynomial below:
We can't use the Quadratic Formula to find the roots, but we can use the Rational Root Theorem to try and find them. The Rational Roots Theorem tells us that IF there's a rational root (a root that's an integer or fraction), then it must be in the form p/q, where p is a factor of the constant term and q is a factor of the leading coefficient. In this polynomial, the leading coefficient is 1 and the constant is -12. This gives us some possible roots to try.
Step 1: Identify possible rational roots.
The factors of -12 are: 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12, -12
The factors of 1 are: 1, -1
When the leading coefficient is 1, it doesn't do much. Dividing the factors of -12 by 1 or -1 just give the same factors already listed. So this means IF the polynomial has a rational root, it's going to be 1, -1, 2, -2, 3, -3, 4, -4, 6, -6, 12, or -12. The Rational Root Theorem doesn't guarantee that one of these will work. A polynomial might only have irrational or imaginary roots. We just know that if there is a rational root, it will be one of the integers listed earlier.
Step 2: Use synthetic division to test possible roots.
Now we need to test these out and see if any of them are actual roots. If we can find the roots of the polynomial, we can use them to write the factors.
How do we test them out? You can use long division if you want to, but it's much faster to use synthetic division. We can test out the possibilities and see if any of them give a remainder of 0. If the remainder is 0, that means it's a root. If the remainder is not 0, cross it off and move on to the next one.
Success! The remainder came out to zero, so we know that -1 is a root of the polynomial. Remember, a root is a value that makes the expression equal to 0. If -1 is a root, that means that (x + 1) is a factor. If we plug -1 into (x + 1), it equals 0.
Step 3: Write two factors.
When you use synthetic division, the bottom row represents the coefficients of the quotient. We started with a degree 3 polynomial and divided by x + 1. This means we're left with a polynomial that's one degree less: a quadratic.
We know that -1 is a root, so (x + 1) must be one of the factors. We can use the coefficients from above to write a second quadratic factor. This means that we can start to factor the polynomial:
So is this the answer? No, but we're almost there. We have to make sure the polynomial is factored completely. If we started with degree 4 or higher, we would need to repeat synthetic division again to find more roots. In this case, we're left with a quadratic that can be factored so we don't need to repeat synthetic division.
Step 4: Factor the remaining quadratic.
Fortunately, quadratics are a little easier to factor. We can use the Quadratic Formula or educated guess-and-check to factor it. This one's not too bad to use educated guess-and-check.
We know the numbers in the LASTS spots have to multiply to -12. That means we'll need one plus sign and one minus sign. We can try 1 and 12, 2 and 6, or 3 and 4. We need to end up with a positive 1x in the middle, so we need (x + 4)(x - 3).
Step 5: Write the final factored answer.
We need to use all 3 roots to write the final factored answer. The number of factors should always match the degree of the polynomial. If the polynomial is degree 3, there will be 3 factors. If it's degree 4, there will be 4 factors, etc.
Example
Step 1: Identify possible rational roots.
When the leading coefficient is 1, you can just look at the factors of the constant term. This means the possible rational roots are 1, -1, 3, -3, 5, -5, 15, -15, 25, -25, 75, or -75.
Step 2: Use synthetic division to test possible roots.
You need the remainder to be 0 in order for the number to be a root. If you get a remainder that's not 0, cross it off and move on to the next option.
The first two didn't work. Keep trying.
Found one! -3 is a root, that means that (x + 3) is a factor. When you use synthetic division, the bottom represents the coefficients of the quotient. This gives us another factor of the polynomial.
Step 3: Write two factors
We know that (x + 3) is one factor because -3 is a root. We can use the coefficients in the bottom row to write a second factor. In this case, our second factor is a quadratic. If your second factor is degree 3 or higher, you will need to repeat synthetic division to try and find more rational roots.
Step 4: Factor the remaining quadratic.
We're not quite done because we need to factor the quadratic next. This is a quadratic that can't be factored through guess-and-check so we need to use the Quadratic Formula to find the roots. Once we know the roots, we'll be able to write the factors.
In this problem, we ended up with a negative number under the square root. If this happens, you need to factor out the square root of -1 and replace it with the imaginary number i. Now that we have the roots for the quadratic, we can write the final factors.
Step 5: Write the final factored answer.
Practice
Want to try factoring a few polynomials on your own? Click the START button below to take a practice quiz.
|
Powered by Interact |