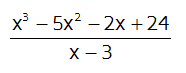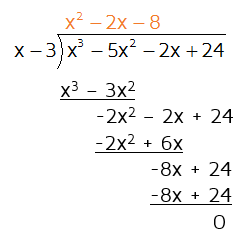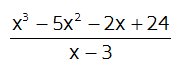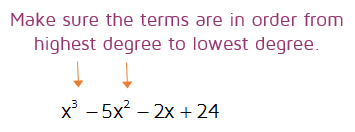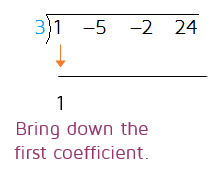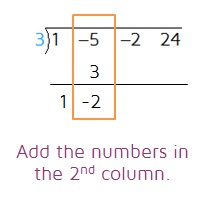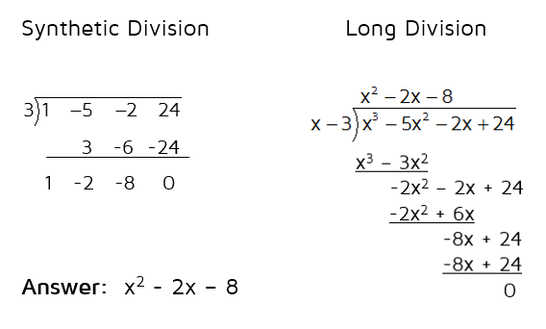|
Accompanying Resource: Printable Study Guide Why Do We Need Synthetic Division?Synthetic division is often used to find the roots of higher-degree polynomials (degree 3 and up). These roots can be used to factor the polynomial.
Let's say you have a quadratic function (degree 2) and you need to find the roots. The roots of a function are the values that make the function equal to zero. On a graph, they are where the function crosses the x-axis. There are several different ways to find the roots of a quadratic function. You could try factoring it or you could complete the square. There's always the Quadratic Formula too. But what if you have a function with a higher degree? If you have an x cubed term or an x to the 4th power, you can't use the Quadratic formula. You could try to factor them, but if the answer is an irrational or complex number you're just out of luck. Thankfully, there is still a way to find the roots or factor a polynomial with a higher degree. It involves dividing the polynomial by a linear factor with a leading coefficient of 1 like x + 4 or x - 3. You could use long division to do this, but synthetic division is a shortcut method that involves only the coefficients of the terms. You get the same answer you would get if you used long division, but most students find that it's much, much faster. It may look complicated at first, but you'll get the hang of it after a few tries. Review of Long DivisionIn order to make sense of synthetic division, let's look at the steps involved in long division. Let's say we have the division problem below:
The first thing you would do is rearrange it and put the x - 3 out to the left. If you use long division to solve this, you get: We see that the answer (in orange) is a quadratic and there is a remainder of 0. Long division can be tricky. You have to be very careful when subtracting negatives and have to make sure you bring down the terms correctly.
Thankfully, synthetic division is a much simpler, faster way to divide polynomials. Using Synthetic Division |
|
So how does synthetic division work? Synthetic division is a shortcut to long division. It's a method that uses only the coefficients of the terms to save time.
Synthetic division can only be used if you're dividing by a LINEAR factor in the form x - a.
For example, it works if you are dividing by x - 3 or by x + 4. If you need to divide by a polynomial with a higher degree or one that doesn't have a 1 as the leading coefficient, you'll have to do plain old long division.
At first glance it may seem a little complicated, but most students can get the hang of it fairly quickly. We'll go step by step and solve the same problem we did earlier, this time using synthetic division.
Division Problem:
Synthetic division can only be used if you're dividing by a LINEAR factor in the form x - a.
For example, it works if you are dividing by x - 3 or by x + 4. If you need to divide by a polynomial with a higher degree or one that doesn't have a 1 as the leading coefficient, you'll have to do plain old long division.
At first glance it may seem a little complicated, but most students can get the hang of it fairly quickly. We'll go step by step and solve the same problem we did earlier, this time using synthetic division.
Division Problem:
Step 1: Make sure the terms of the numerator are in descending order. If a term is missing, add it in with a coefficient of 0.
Step 1: Make sure the terms of the numerator are in descending order. If a term is missing, add it in with a coefficient of 0.
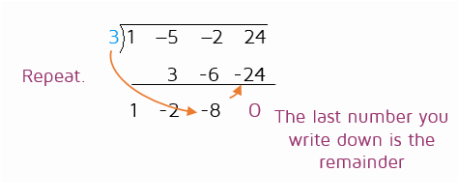
Step 2: Set the denominator equal to 0 and solve to find the number to put as the divisor. When you use long division, you subtract at each step. Synthetic division uses addition instead, so we switch the sign to account for this. If you're dividing by x - 4, you'll use a positive 4. If you're dividing by x + 5, you'll use a -5.
Step 3: Set up the problem using only the coefficients of each term in the numerator.
Step 4: Bring down the first coefficient. When you're dividing by x - a, the first coefficient will always stay the same.
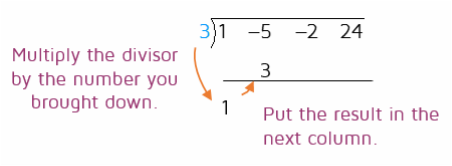
Step 5: Multiply the divisor by the number you brought down. Put the result in the next column.
Step 6: Add the numbers in the 2nd column. In long division, you subtract. With synthetic division, we switch the sign when we write the divisor so that we can add.
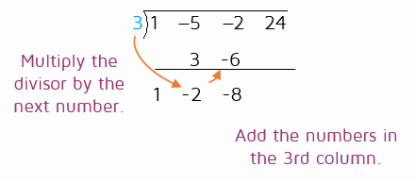
Step 7: Repeat. Multiply the divisor by the new number you wrote down and put the result in the next column. Repeat this process until you run out of columns. The last number you write down is the remainder.
Step 8: Write the answer. The numbers you wrote down on the bottom row are the coefficients of the answer. The last number on the right is the remainder. In synthetic division, you're always dividing by a linear factor in the form x - a, so the degree of your answer will always be one less than what you started with. For example, if the numerator had degree 4, then the answer would be degree 3. In this example, the numerator had degree 3, so our answer is a degree 2.
Let's take a look at the two methods side by side. Synthetic division certainly takes up less space and the more you do it, the faster you'll get. Both methods give the same answer.
Practice
Want to try some problems on your own? Click the START button below to try a practice quiz.