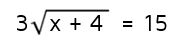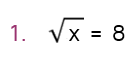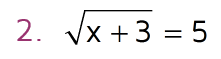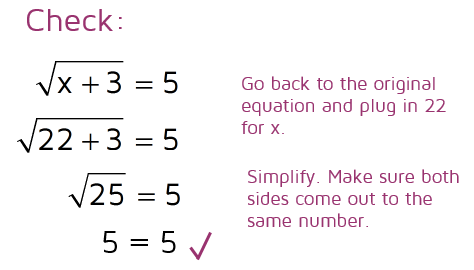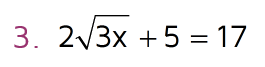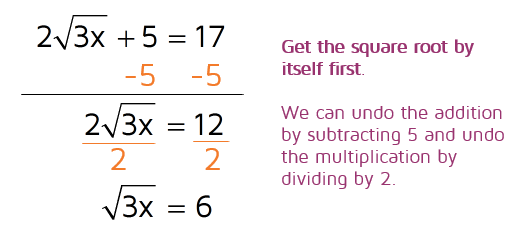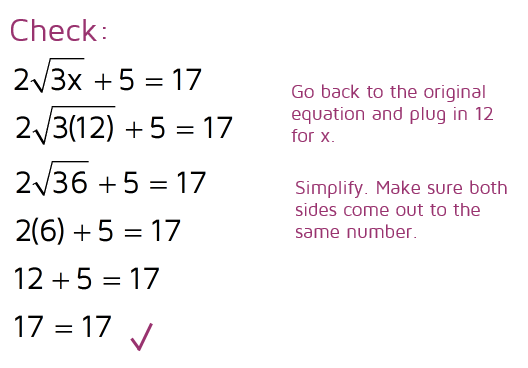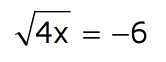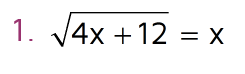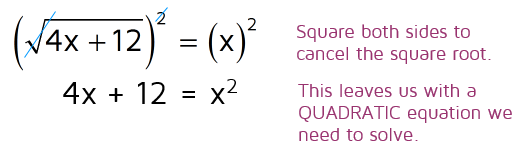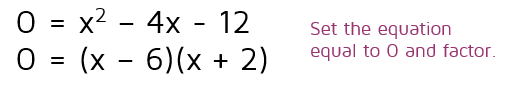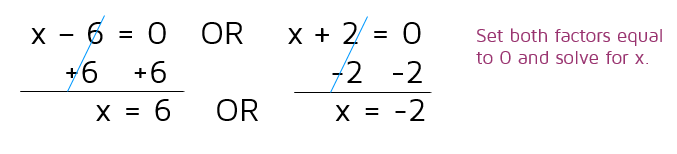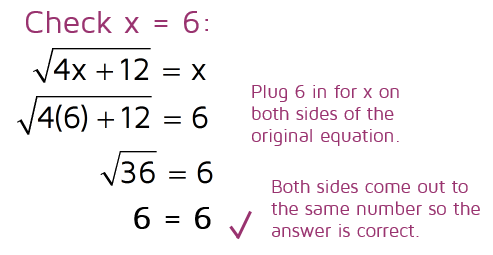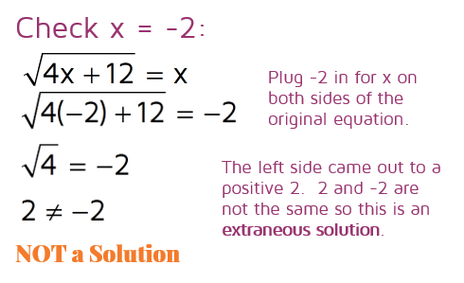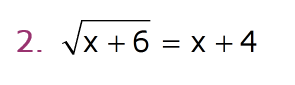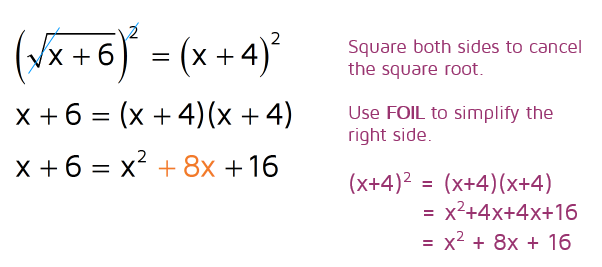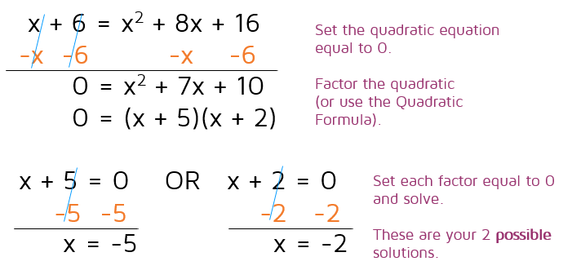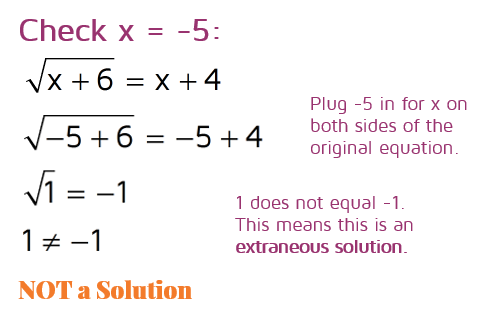|
|
It's pretty easy to check your answer on this one. Does the square root of 64 equal 8? Yes. The answer is correct.
Here's a radical equation that's just a little harder
In this equation, if you add 3 to x and then take the square root, the answer will be 5. We need to work our way backwards to solve for x. First, we need to undo the square root. We can cancel a square root by squaring both sides. When you square the left side, the square root sign just cancels out and you're left with the x + 3 that was inside it.
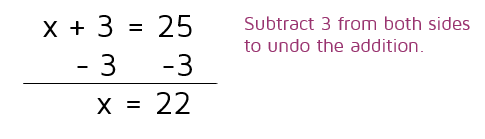
After we undo the square root, we're left with a pretty simple equation to solve. To undo addition, we use the inverse operation and subtract 3 from both sides to get x by itself.
It's always a good idea to check your answer if you can. To see if 22 is the correct answer, we need to plug it in for x in the original equation. If we add 3 and then take the square root, we get the square root of 25. The square root of 25 does come out to 5, so we have the correct answer.
Let's try one with a few more steps:
When you solve an equation, think about it as working your way backwards to figure out what x is. If you knew what x was and were plugging it in, you would multiply it by 3 first, then take the square root, multiply that number by 2 and then add 5 last. We need to go backwards now and undo all those steps to find x. When you see a square root in your equation, don't automatically square both sides first. In this situation, the 5 was added last so our first step needs to be to subtract 5 from both sides.
It can be helpful to pretend the radical part is just an x and think about the steps you would take to get the x by itself. For example, if you had the equation 2x + 5 = 17 you would subtract 5 first and then divide by 2.
Once you have the radical by itself on side of the equation, you can undo the square root by squaring both sides.
Check your answer by plugging 12 in for x in the original equation. Follow the order of operations to simplify the left side and make sure it really does equal 17 if you plug in your answer.
It works! This means 12 is the correct answer.
Extraneous Solutions
I didn't exactly tell the whole truth above about checking your answer. It's of course always good to check your answer whenever possible, but if your equation involves a radical you MUST check your answer. Why? When you square both sides of an equation, it sometimes creates "solutions" that don't actually work. Here's an example:
We can go through the steps to solving this equation
We didn't make any mistakes when we solved this problem. All the steps are accurate. But look what happens when we go to check our answer:
This is an example of what's called an extraneous solution. Sometimes in the process of solving an equation, you come up with an answer that doesn't actually work. This can happen when you're dealing with radicals in your equation.
Why does this happen? It's a little tricky to explain, but here's a simple example.
Look at what happens when we square both sides. We started with two numbers that were not equal, and ended up with two numbers that are equal.
When you square both sides of an equation, it can create "extra" solutions that aren't really solutions. Some equations will have "No Solution" because the equation that you started with was actually false. By squaring both sides, you created an extraneous solution that doesn't actually work when you plug it in. This means that it is crucial to always check your answers when solving radical equations to weed out any "extra" answers.
How do you know if an answer is extraneous? Always plug your answer back into the original equation. If the answer is extraneous, the two sides of the equation will come out to two different numbers.
Radical Equations with
Variables on Both Sides
If your radical equation involves variables on both sides, it's a little trickier to solve. Let's look at some examples that are a little harder than the ones above.
The radical is by itself on the left side, so our first step is to square both sides. This will cancel the square root sign and we're left with what's inside the radical.
Sometimes when you square both sides, you end up with a quadratic equation. There are a few different ways to solve quadratic equations. The fastest way is usually to set it equal to 0 and try to factor it. If that doesn't work, you can use the Quadratic Formula to solve the equation.
Once you've factored a quadratic, you can use the Zero Product Property and set each factor equal to 0. This gives us two possible answers.
The temptation is to stop here and say the two answers are 6 and -2. The problem is that one or both of them might be extraneous solutions. We need to plug in the possible answers and see if they are actual solutions or not. Make sure to always go back to the original equation to check your answers.
It works when we plug it in for x so 6 is a solution. Now we need to check the second possible answer.
This one does not work. This means -2 is NOT a solution. This problem only has one answer: x = 6.
Let's try one more with variables on both sides.
The radical is already by itself on the left side of the equation, so our first step is to square both sides to cancel the square root. This is the step where you need to be very careful. There are two terms on the right side. If you square x + 4, you don't just square the x and square the 4. You need to multiply the binomial by itself and use FOIL to simplify it.
Be careful! Students often make a mistake at this step and miss the middle term. Don't just square the x and square the 4. Make sure to square the entire binomial and use FOIL to simplify.
We're left with a quadratic equation now that we need to solve. Remember, you can solve quadratic equations by setting the equation equal to zero and factoring or using the Quadratic Formula.
So we have two possible solutions: x = -5 or x = -2. They might both work, only one might work, or they might both be extraneous solutions. The only way to tell is to plug them both back into the original equation and see. If both sides come out to the same number, it's a solution. If you plug it in and the left and right side come out to different answers, it's not a solution. Be extra careful when negative numbers are involved. Students tend to make sign errors here, so it might be a good idea to double check your work with a calculator if you can.
When we plugged in -5 for x, it did not work. The two sides came out to different numbers. This tells us that -5 is an extraneous solution. Now we need to check the second possible answer (x = -2) and see if that one works.
This one works. Both sides simplified to the same answer, so this tells us x = -2 is a solution.
Radical Equations Video
Want to see another example? Check out the short video below.
Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.
|
Powered by Interact |
Want to learn how to solve a logarithmic equation or exponential equation?