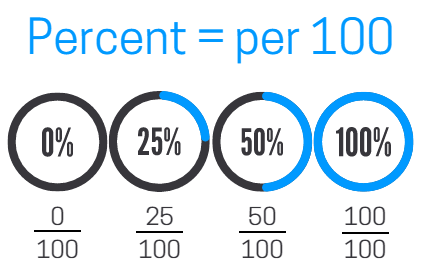
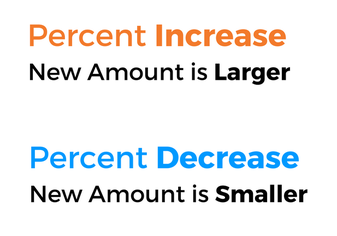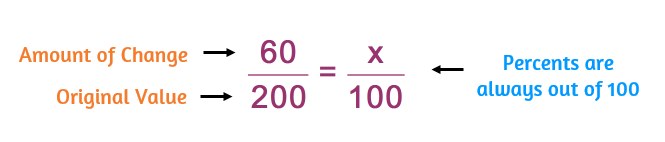What is a Percent?The word percent means "per 100." We often use percents to describe a part of a whole. For example, 75% means 75 out of 100, 14% means 14 out of 100. The diagram below has a few examples of commonly used percents.
|
|
Percent of Increase and Percent of Decrease
It's pretty straightforward to determine if the change is an increase or a decrease. If the new amount is larger than the original, it's called a "percent of increase" or "percent increase." If the new amount is smaller than the original, it's called a "percent of decrease" or "percent decrease."
How Do You Calculate a Percent of Change?
There's more than one way to calculate a percent of increase or decrease. If you google how to find the percent of change, chances are you'll find a list of steps to follow. It's easy to follow these steps while you're doing an assignment without really thinking about why the steps work. Make sure to try and understand the steps so it's not just a process you try to memorize and quickly forget.
Using Proportions to Calculate Percent of Change
One way to find a percent of change is to use a proportion. Remember, a percent means "per 100." You can describe the change as a fraction comparing the amount of change to the original and then use a proportion to rewrite your problem as a percentage out of 100.
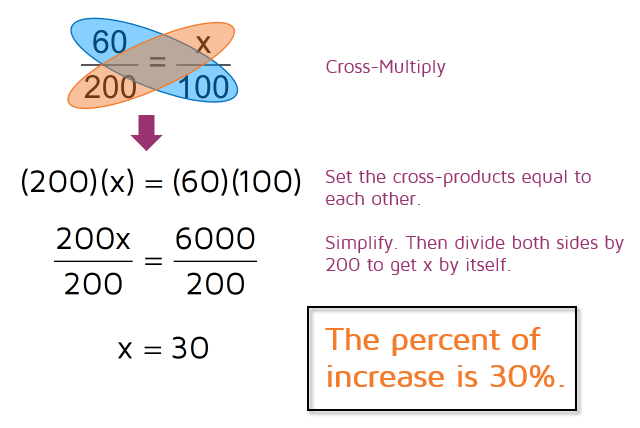
Let's start with an example. Say the price of a stereo increased from $200 to $260. This means the price increased by $60. In this example, the price increased $60 from the original $200. This gives you the fraction 60/200. When you describe a change as a percentage, always describe it in comparison to the original amount.
A percent is always out of 100. We can use the proportion below to find the percent, the proportion just allows us to rewrite the fraction as a number out of 100. We know that 60 out of 200 is the same as the percent out of 100.
Let's start with an example. Say the price of a stereo increased from $200 to $260. This means the price increased by $60. In this example, the price increased $60 from the original $200. This gives you the fraction 60/200. When you describe a change as a percentage, always describe it in comparison to the original amount.
A percent is always out of 100. We can use the proportion below to find the percent, the proportion just allows us to rewrite the fraction as a number out of 100. We know that 60 out of 200 is the same as the percent out of 100.
Next, you can cross-multiply to solve for x. (Not sure how? Check out the lesson on solving proportions if you need help with this step.)
Remember to look back and see if the new amount is larger or smaller than the original. In this example, the price went up so this is a percent of increase.
Using Decimals to Calculate Percent of Change
You can also use a decimal to help you find a percent of change. Make sure to check out the lesson on converting between percents, decimals, and fractions if you need a refresher. To do this, start by describing the change as a fraction comparing the amount of change to the original value.
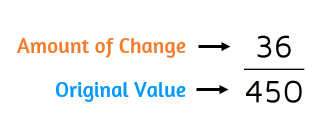
Let's say a school had 450 students last year and now has 414 students. This means there was a change of 450-414=36 students. The new number is smaller, so we'll be finding the percent of decrease this time. The steps are the same no matter if it's an increase or decrease. The percent of change is always written as a positive number. Make sure to always subtract the smaller number from the larger number to find the amount of change.
When you write the fraction, make sure to always compare the change to the original amount. In this example, the change is 36 students compared to an original 450 students. This gives us the fraction 36/450.
Let's say a school had 450 students last year and now has 414 students. This means there was a change of 450-414=36 students. The new number is smaller, so we'll be finding the percent of decrease this time. The steps are the same no matter if it's an increase or decrease. The percent of change is always written as a positive number. Make sure to always subtract the smaller number from the larger number to find the amount of change.
When you write the fraction, make sure to always compare the change to the original amount. In this example, the change is 36 students compared to an original 450 students. This gives us the fraction 36/450.
You could go ahead and set this equal to x/100 if you want to use a proportion to solve it. A different way to change it to a percent is to convert the fraction to a decimal first and then change it to a percent. To change 36/450 to a decimal, you simply divide 36 by 450 on a calculator. This gives you the decimal .08. Do you see that the 8 is in the hundredths place? The decimal .08 means 8 hundredths, or 8/100. This means the percent of decrease is 8%. You can also use the shortcut to change a decimal to a percent and simply move the decimal over two places to the right.
Percent of Change Practice
Ready to try some problems on your own? Click the START button below to take a practice quiz.
Want to learn more about percents?
Check out the lesson on finding the percent of a number.
Check out the lesson on finding the percent of a number.