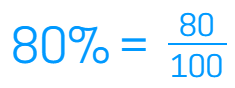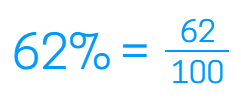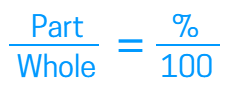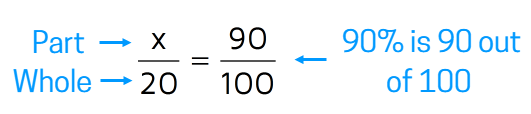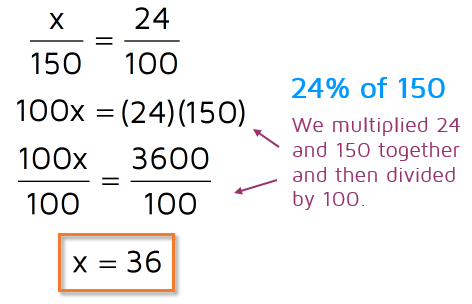Accompanying Resources: 
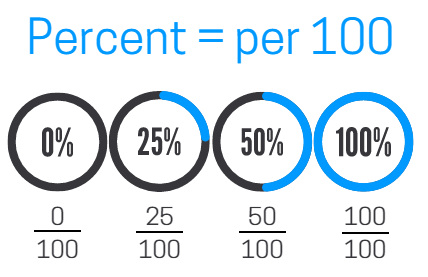
Google Drive Activity, ​Printable & Digital Study Guide, Boom Cards (digital task cards)

What is a Percent?

The word percent means "per 100."  We often use percents to describe a part of a whole.  For example, 75% means 75 out of 100, 14% means 14 out of 100.  The diagram below has a few examples of commonly used percents.  

Percent of a Number

Let's say you took a test with 100 questions.  If you scored an 80% on the test, what does that mean?  80% means 80 out of 100.  An 80% on a test with 100 questions means you got 80 correct out of a total of 100.

It's pretty easy to find the percent of a number if the total is already out of 100.  Let's say you ended up with exactly 100 pieces of candy after Halloween.  If 62% of the candy is chocolate, what does that mean?  62% means 62 out of 100.  If you have 100 pieces of candy total, then 62 of those are chocolate.

What you've just done is called finding the percent of a number.  This was a pretty simple case where the total was out of 100.  62% of 100 is just 62.

Welcome to Kate's Math Lessons!  

Teachers: make sure to check out the study guides and activities.

Here's another example when the total is out of 100.  Let's say 100 students took a survey.  If only 20% of the students said they like to wake up early, how many students is that? 20% means 20 out of 100, so 20 of the students said they like to wake up early.  In other words, 20% of 100 is just 20.

So what do you do if the total isn't out of 100?  What if only 50 students took the survey? How would you find 20% of 50?  It's not quite as simple as the two examples above, but you can still find the percent of a number even when the total isn't out of 100.  There's more than one way to do it.  We'll look at two different ways in this lesson and you can use whichever one seems easiest to you!

Using a Proportion to find
​the Percent of a Number

A percent is out of 100, so what do you do if the total isn't 100?  One way to find a percent of a number is to use a proportion.  A proportion basically allows us to change the problem so the total is out of 100.  Remember, a percent is really just a fraction. It's how many you have out of 100.  If you have a total that isn't 100, you can solve the proportion to figure out the percent of a number.

Let's say you got a 90% on a test.  If the test had 100 questions, this would mean that you got 90 correct out of 100.  What if the test only had 20 questions? How many did you get right?We need to find 90% of 20.  We can set this up as a proportion: what number out of 20 is the same as 90 out of 100?

There's more than one way to solve a proportion. Check out the lesson on solving proportions if you need extra help with this step.  One easy way to solve a proportion is to cross-multiply.

This means that 90% of 20 is equal to 18.  Another way to say this is if you get 18 out of 20 right on a quiz, you got 90% of the questions correct.  You can double check this by changing the fraction 18/20 to a decimal.  (Not sure how? Check out the lesson on converting between percents, decimals, and fractions)  

Here are a few more examples to help you understand how to use a proportion to find a percent of a number:

Example 1

Find 70% of 40.

Pretend we just surveyed 40 people and 70% of them said that pizza is their favorite food.  If we had surveyed 100 people total, that would mean 70 out of the 100 chose pizza.  But we only surveyed 40, not 100.  We can use a proportion to figure out how many people out of 40 would be the same as 70 out of 100.  

The hardest part is setting up the proportion. Now we can cross-multiply to find the answer. Make sure to check out the lesson on solving proportions if you need help with this step.

This means that 70% of 40 is equal to 28.   Another way to say this is that 28 out of 40 is the same as 70 out of 100.  You can double check this by changing the fraction 28/40 to a percent and make sure it comes out to 70% (check out the lesson on converting between percents, decimals, and fractions if you need help with this step).

Example 2

Find 24% of 150.

Let's say you ended up with 150 pieces of candy after Halloween and 24% have chocolate in them.  If you had exactly 100 pieces, 24% of 100 would be 24 pieces.  So if you increase the total to 150, what would 24% of that be?  You can use a proportion to set this up. How many pieces out of 150 is the same as 24 out of 100?

Now you can cross-multiply to find the answer.

This means that 24% of 150 is 36.  Another way to say this is that 36 out of 150 total is the same as 24 out of 100.  You can double check this by changing the fraction 36/150 to a percent and make sure it comes out to 24%.


Now let's look at a different method that can be used to find the percent of a number.

Multiplying by a Decimal to Find the Percent of a Number

If we look back at how we solved the last few problems with the proportion method, we can start to see a pattern.  Did you notice that each time we multiplied the two numbers together and then divided by 100?

We ended up dividing by 100 each time because percents are always out of 100.  If you set up a proportion to find the percent of a number, you'll always end up dividing by 100 in the end. 

Another way to get the same answer is to divide by 100 first and then multiply the numbers together.  24/100 = .24  and (.24)(150) = 36.  This is the same answer we got by cross-multiplying.  Most people prefer this method to setting up a proportion because it's a little bit faster, but you can chose to find the percent of a number either way.  Both methods result in the same answer.

When you divide the percent by 100, you're just changing it to a decimal. Remember, dividing by 100 just moves the decimal over two places to the left.  

Remember that a percent is always out of 100.  To change a percent to a decimal, you just need to divide it by 100.  This will move the decimal over two places to the left.  For example, 5% is the same as 5/100.  This becomes .05 as a decimal.  82% is the same as 82/100, which is .82 as a decimal.

Example 1

Find 32% of 75.

Step 1: Change 32% to a decimal.  32% is the same as 32/100, which is .32 as a decimal.
Step 2: Multiply.   (.32)(75) = 24

This means that 32% of 75 is 24.

Example 2

Find 8% of 250.

Step 1: Change 8% to a decimal.  8% is the same as 8/100, which is .08 as a decimal.  
Step 2: Multiply.  (.08)(250) = 20

This means that 8% of 250 is 20.

Be extra careful when the percent is less than 10%! A common mistake on this problem is to accidentally write 8% as .8 instead of .08.  If you use .8 on accident, you would find 80%, not 8%. Always think about the reasonableness of your answer.  8% means 8 out of every 100. That's not very much so we should have expected a small number in comparison to a total of 250. 

Now that you've seen two different ways to solve a proportion, it's up to you which method you would like to use. Both methods will result in the same answer.  

Practice

Ready to try a few problems on your own? Click the START button below to take a practice quiz.

Powered by