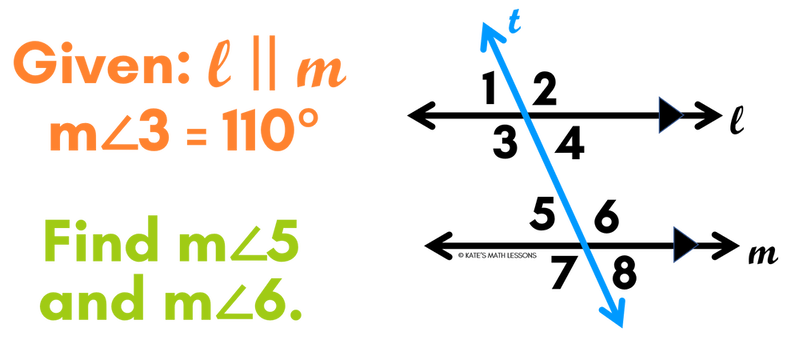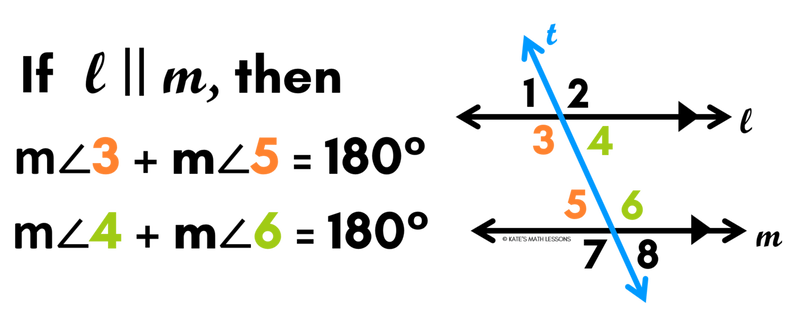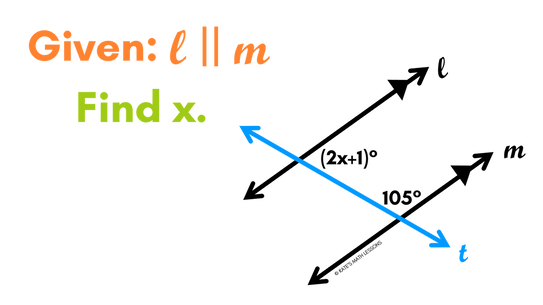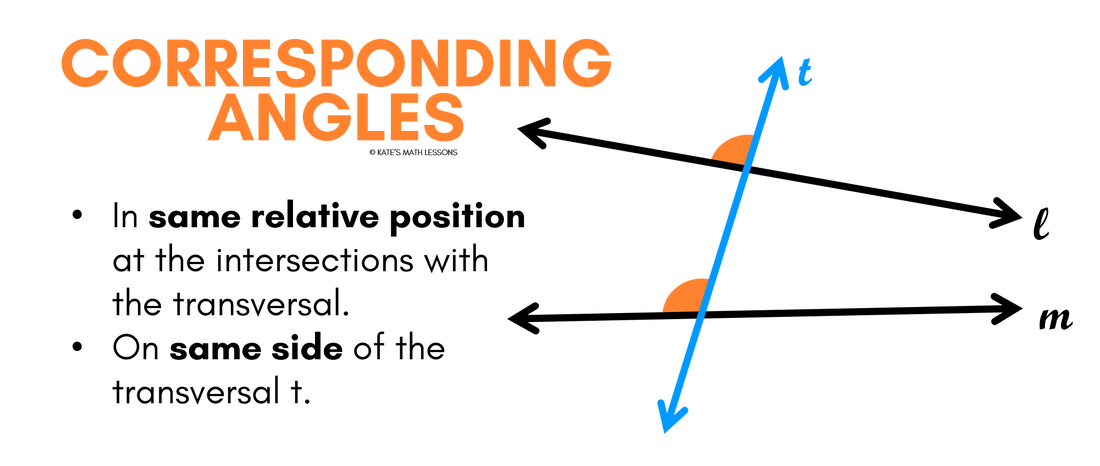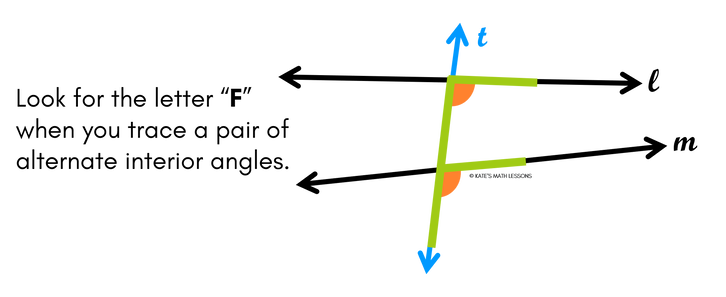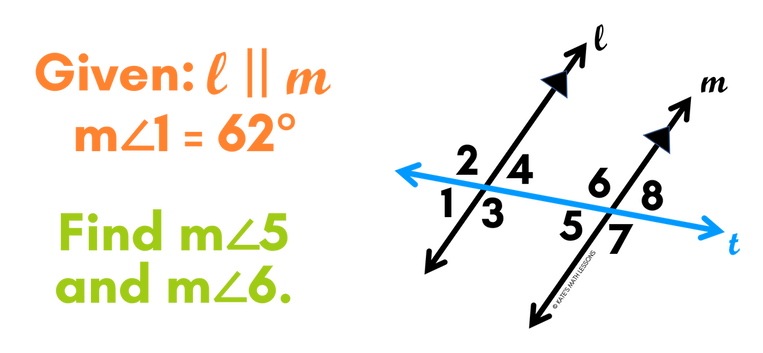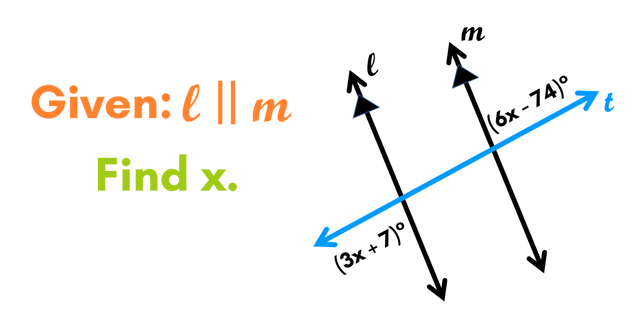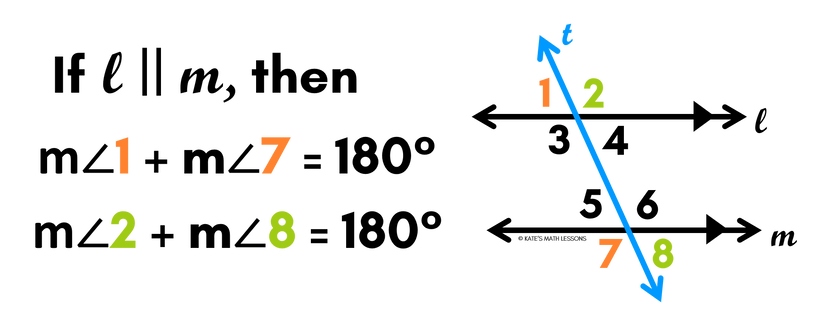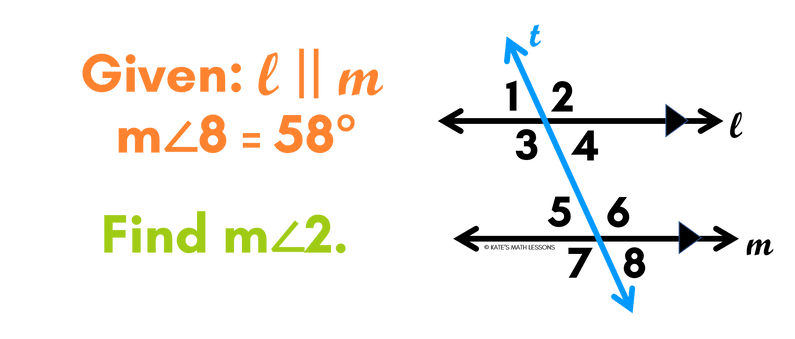Accompanying Resources:
Parallel Lines, Transversals and Angle Pairs Digital Activity for Google
Parallel Lines Cut by a Transversal Activity: Digital Boom Cards
Parallel Lines, Transversals and Angle Pairs Digital Activity for Google
Parallel Lines Cut by a Transversal Activity: Digital Boom Cards
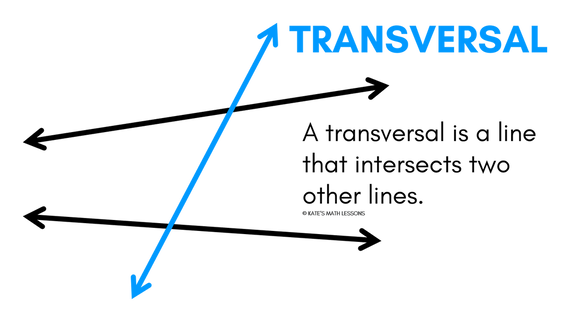
What is a Transversal?
In geometry, a transversal is a line that crosses two other lines in the same plane. The transversal will intersect (or cross) the two lines in two points.
The lines can be going in any direction, so a transversal can be shown to be closer to a vertical line like in the picture above, or a transversal can also be closer to a horizontal line like the picture below. You can always just rotate your paper around if you prefer to look at it one way over another.
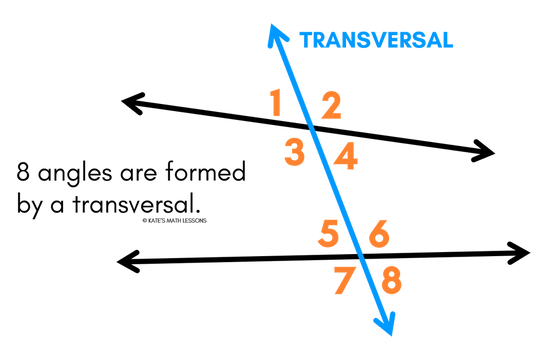
Angles Formed by a Transversal
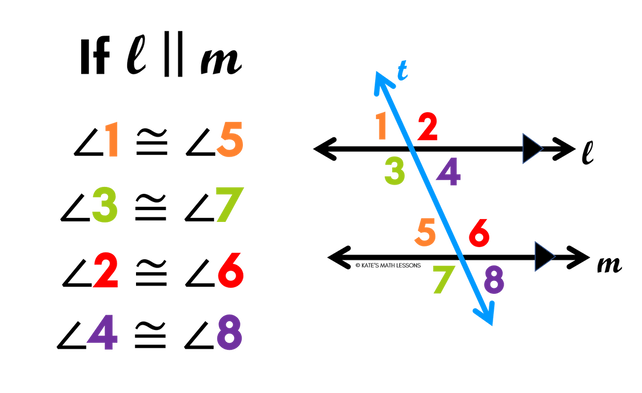
When a transversal crosses two other lines, 8 different angles are formed. You can see 4 angles formed by the transversal and the top line and 4 different angles formed by the bottom line.
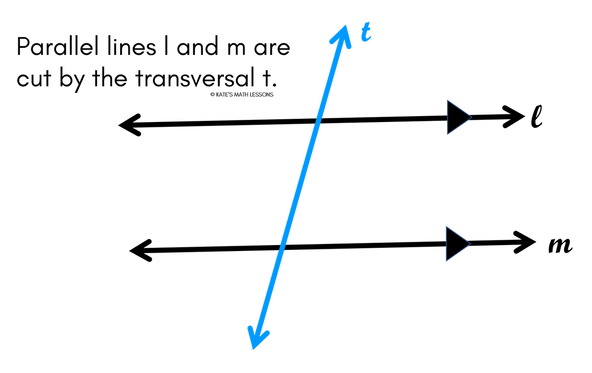
Parallel Lines Cut by a Transversal
What does parallel lines cut by a transversal mean? When you hear this, it just means that the two lines that have been crossed by the transversal are parallel to each other (lines that will never cross). In the diagram below, lines l and m are parallel and they are "cut" by the transversal t.
If you see extra arrows on a line like on lines l and m above, they indicate that the two lines are parallel. You may also be told at the beginning of math problem that lines are parallel using the symbol with two vertical lines like below:
Angle Pairs formed by a Transversal
There are several different special angle pairs that are formed by a transversal. The names of these pairs apply for any two lines that are being crossed by a transversal, but typically they're most helpful when the two lines are parallel. When parallel lines are cut by a transversal, several different pairs are formed that are either congruent to each other (have the same angle measure) or the angle pairs might be supplementary angles (angles that add up to 180 degrees). Knowing the properties of the different angle pairs can be helpful to find missing angles in a diagram.
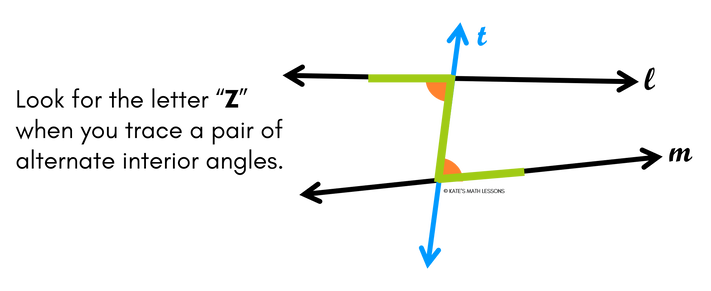
Alternate Interior Angles
The first pair of angles we'll look at are called Alternate Interior Angles. They're on opposite sides of the transversal and they're in on the inner side of the two lines that are being cut by the transversal.
There are two sets of alternate interior angles formed when two lines are cut by a transversal. To find alternate interior angles, look on the inside of the two lines that are being crossed and find the angles that are on opposite sides of the transversal. One way to help you identify alternate interior angles is to trace the two angles and see if they form the letter "Z" (or a backwards/sideways Z).
Alternate Interior Angles Theorem
If two parallel lines are cut by a transversal, the alternate interior angles are congruent.
Make sure to note that the alternate interior angles are only congruent if the transversal is crossing two parallel lines. If a transversal crosses two lines that are not parallel, the alternate interior angles will NOT be congruent.
Alternate Interior Angles Example
We can use the Alternate Interior Angles Theorem to find missing angles in a diagram. See if you can find the missing angles in the problem below. Then scroll down to see if your answers are correct.
ANSWER:
We know that angles 3 and 6 are a pair of alternate interior angles. We also know that lines l and m are parallel, which means that the alternate interior angles are congruent. This means that the measure of angle 6 is also 110 degrees.
If you look closely at angles 5 and 6, you can see that they form a straight line, which means they are a linear pair and their measures must add up to 180 degrees. So to find the measure of angle 5, we can subtract the measure of angle 6 from 180. 180-110 = 70. This means the measure of angle 5 is 70 degrees.
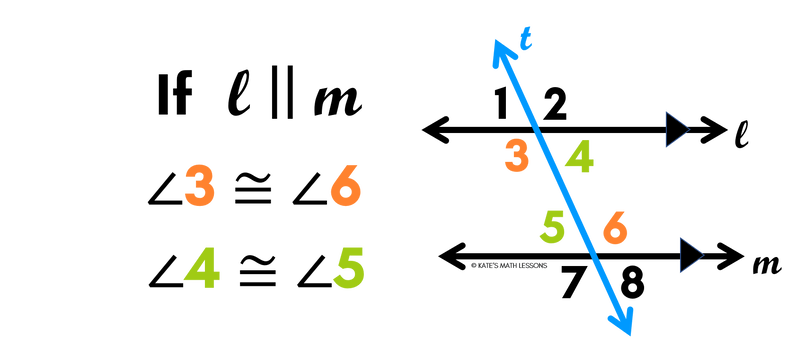
Consecutive Interior Angles (Same Side Interior Angles)
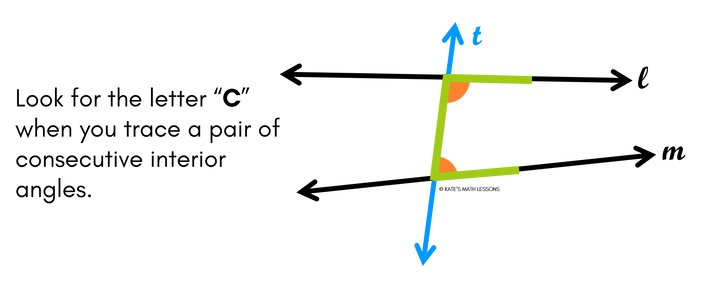
The next pair of angles we'll look at are called consecutive interior angles. These are also sometimes called Same Side Interior Angles. It helps to know that the word "consecutive" often means in a row, or right next to each other. Consecutive interior angles are also on the inner side of the two lines that are being crossed, but this time they're on the same side of the transversal.
There are two sets of consecutive interior angles. To find consecutive interior angles, look on the inside of the two lines that are being crossed and find the angles that are on same side of the transversal. One way to help you identify consecutive interior angles is to trace the two angles and see if they form the letter "C" (or a backwards/sideways C).
Consecutive Interior Angles Theorem
If two parallel lines are cut by a transversal, the consecutive interior angles are supplementary.
There are two very important parts of this theorem to pay attention to. First, this statement is only true if the two lines that the transversal is crossing are parallel. Second, note that the consecutive interior angles will be supplementary, not congruent. Supplementary means their angle measures are going to add up to 180 degrees.
Consecutive Interior Angles Example
We can use the Consecutive Interior Angles Theorem to find missing angles in a diagram. See if you can find the missing angles in the problem below. Then scroll down to see if your answers are correct.
ANSWER:
We know that lines l and m are parallel, this means that consecutive interior angles are going to be supplementary (their angle measures will add up to 180 degrees). The two angles marked in the diagram are on the inner side of lines l and m and are on the same side of the transversal t, so they are consecutive interior angles. This means that when we add the two angle measures together, they need to add up to 180. We can use this to set up the equation: (2x + 1) + 105 = 180. To solve this, we can simplify the left side of the equation to get 2x + 106 = 180. Then subtract 106 from both sides to get 2x = 74. Last, divide both sides by 2 to get x = 37.
We know that lines l and m are parallel, this means that consecutive interior angles are going to be supplementary (their angle measures will add up to 180 degrees). The two angles marked in the diagram are on the inner side of lines l and m and are on the same side of the transversal t, so they are consecutive interior angles. This means that when we add the two angle measures together, they need to add up to 180. We can use this to set up the equation: (2x + 1) + 105 = 180. To solve this, we can simplify the left side of the equation to get 2x + 106 = 180. Then subtract 106 from both sides to get 2x = 74. Last, divide both sides by 2 to get x = 37.
Need more help solving equations like the one above? Make sure to check out my Solving Two-Step Equations Lesson.
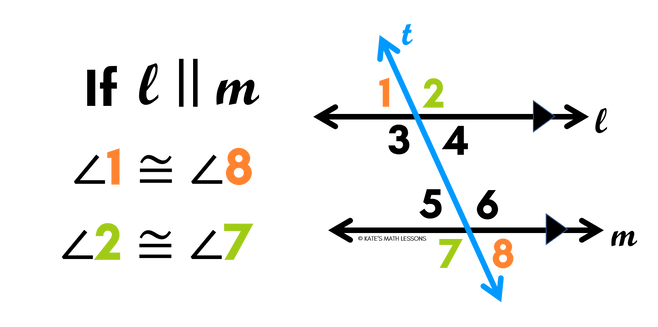
Corresponding Angles
The next pair of angles we'll look at are called corresponding angles. They're a little tricky to describe in words, but they're angles that are in the same relative position at the two intersections of the lines and the transversal. For example, in the image below the first angle is in the top left position where the first line crosses the transversal. Its corresponding angle is also in the top left position where the second line crosses the transversal.
There are four sets of consecutive interior angles, two on each side of the transversal. To find corresponding angles, look on the same side of the transversal and choose the angle that's in the same "spot" as the first one (for example, both in the bottom right position at the intersections of he lines).
One way to help you identify corresponding angles is to trace the two angles and see if they form the letter "F" (or a backwards/sideways F).
One way to help you identify corresponding angles is to trace the two angles and see if they form the letter "F" (or a backwards/sideways F).
Corresponding Angles Postulate
If two parallel lines are cut by a transversal, the corresponding angles are congruent.
If the transversal is crossing two lines that are parallel, the angles in the same relative positions at the intersections are going to be congruent (have the same angle measure).
Corresponding Angles Example
We can use the Corresponding Angle Postulate to find missing angles in a diagram. See if you can find the missing angles in the problem below. Then scroll down to see if your answers are correct.
ANSWER:
If you look at the first intersection on the left where line l intersects transversal t (angles 1-4), you can see that angle 1 is in the bottom left position. This means that its corresponding angle is in the bottom left position in the second intersection where line m intersects transversal t. This is angle 5 (notice if you trace angles 1 and 5, they would form the letter F on its side).
Since lines l and m are parallel, the Corresponding Angles Postulate tells us that angles 1 and 5 must be congruent so the measure of angle 5 is also 62 degrees.
We can also see that angles 5 and 6 are a linear pair (they form a straight line), which means their angle measures add up to 180 degrees. To find the measure of angle 6, we can subtract 62 degrees from 180 degrees. 180 - 62 = 118. This means the measure of angle 6 is 118 degrees.
If you look at the first intersection on the left where line l intersects transversal t (angles 1-4), you can see that angle 1 is in the bottom left position. This means that its corresponding angle is in the bottom left position in the second intersection where line m intersects transversal t. This is angle 5 (notice if you trace angles 1 and 5, they would form the letter F on its side).
Since lines l and m are parallel, the Corresponding Angles Postulate tells us that angles 1 and 5 must be congruent so the measure of angle 5 is also 62 degrees.
We can also see that angles 5 and 6 are a linear pair (they form a straight line), which means their angle measures add up to 180 degrees. To find the measure of angle 6, we can subtract 62 degrees from 180 degrees. 180 - 62 = 118. This means the measure of angle 6 is 118 degrees.
Need more help solving equations like the one above? Make sure to check out my Solving Equations with Variables on Both Sides Lesson.
Alternate Exterior Angles
The next pair of angles we'll look at are called alternate exterior angles. We looked at alternate interior angles earlier, so these are similar except this time they're on the outside of the two lines being crossed by the transversal.

Unfortunately, I don't have an easy letter for you to remember this type of angle relationship. Try to remember that the word "alternate" tells you they're on opposite sides of the transversal and the word "exterior" tells you they're on the outside of the two lines that are being crossed.
Alternate Exterior Angles Theorem
If two parallel lines are cut by a transversal, the alternate exterior angles are congruent.
Alternate Exterior Angles Example
We can use the Alternate Exterior Angles Theorem to help us find missing angles in a diagram. See if you can find the missing angles in the problem below. Then scroll down to see if your answers are correct.
ANSWER:
We can see that the two marked angles are on opposite sides of the transversal and are on the exterior of lines l and m, so they are alternate exterior angles. We know from the Alternate Exterior Angle Theorem that these two angles are congruent, so their angle measures are equal since lines l and m are parallel. This means we can set up an equation by setting the two angle measures equal to each other: 3x + 7 = 6x - 74. We can solve this by first subtracting 3x from both sides. This gives us 7 = 3x - 74. Next we can add 74 to both sides to get 81 = 3x. Last, divide both sides by 3 to get x = 27.
We can see that the two marked angles are on opposite sides of the transversal and are on the exterior of lines l and m, so they are alternate exterior angles. We know from the Alternate Exterior Angle Theorem that these two angles are congruent, so their angle measures are equal since lines l and m are parallel. This means we can set up an equation by setting the two angle measures equal to each other: 3x + 7 = 6x - 74. We can solve this by first subtracting 3x from both sides. This gives us 7 = 3x - 74. Next we can add 74 to both sides to get 81 = 3x. Last, divide both sides by 3 to get x = 27.
Consecutive Exterior Angles (Same Side Exterior Angles)
The last angle pair relationship we'll look at are angles on the outside of the two lines and this time are on the same side of the transversal. These are called consecutive exterior angles or same side exterior angles.
Sorry, I don't have a letter for this angle pair relationship either, but try to remember that the word "consecutive" tells you they're on the same side of the transversal and the word "exterior" tells you they're on the outside of the two lines being crossed.
Consecutive Exterior Angles Theorem
If two parallel lines are cut by a transversal, the consecutive exterior angles are supplementary
Consecutive Exterior Angles Example
We can use the Consecutive Exterior Angle Theorem to find missing angles in a diagram. See if you can find the missing angles in the problem below. Then scroll down to see if your answers are correct.
ANSWER:
We know that angles 2 and 8 are consecutive exterior angles because they're on the same side of the transversal and on the exterior of angles l and m. Since lines l and m are parallel, this tells us the angles 2 and 8 are supplementary (their angle measures add up to 180 degrees). To find the measure of angle 2, we can subtract 58 degrees from 180 degrees. 180 - 58 = 122. So the measure of angle 2 is 122 degrees.
We know that angles 2 and 8 are consecutive exterior angles because they're on the same side of the transversal and on the exterior of angles l and m. Since lines l and m are parallel, this tells us the angles 2 and 8 are supplementary (their angle measures add up to 180 degrees). To find the measure of angle 2, we can subtract 58 degrees from 180 degrees. 180 - 58 = 122. So the measure of angle 2 is 122 degrees.
Common Mistakes with Angle Pair Relationships
Now that we've looked at all the different angle pair relationships, I want to point out some common mistakes that students make so you can avoid them. Many times, students will forget which pairs are congruent and which pairs are supplementary.
Make sure you're looking carefully at the diagram to see if your answer makes sense. Look at the diagram ahead of time and take note of whether the angle you're looking for appears to be acute, right, or obtuse. This will help you catch some mistakes if you accidentally confuse which pairs are congruent and which pairs are supplementary.
Make sure you're looking carefully at the diagram to see if your answer makes sense. Look at the diagram ahead of time and take note of whether the angle you're looking for appears to be acute, right, or obtuse. This will help you catch some mistakes if you accidentally confuse which pairs are congruent and which pairs are supplementary.
Parallel Lines, Transversals and Angle Pairs Activity
Teachers: Don't miss these accompanying resources to help your students identify angle pairs and find missing angle measures when parallel lines are cut by a transversal. Students love these digital alternatives to a worksheet and both of these angle pair activities are self-grading!