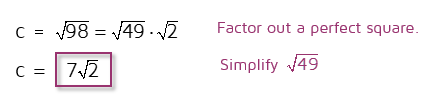|
45-45-90 Triangles Page 2 of 5
Hypotenuse of a 45-45-90 TriangleThe hypotenuse of a 45-45-90 triangle is not quite as easy to find. There's a long way and a short way to find it. The long way is to use the Pythagorean Theorem. We'll briefly look at the long way first and then show you how to use the shortcut.
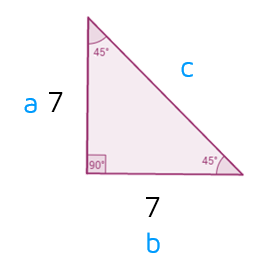
The Long Way: Use the Pythagorean TheoremIf you know both the legs of a right triangle, you can use the Pythagorean Theorem to find the hypotenuse. Remember, a and b are the legs that form the right triangle and c is the hypotenuse.
|
|
We could leave the answer for the hypotenuse as the square root of 98 or round it and get a decimal answer. To show the shortcut relationship, we can simplify the square root of 98 instead. When you're simplifying a square root, look for factors of the number under the square root that are perfect squares. See if you can divide the number by 4, 9, 16, 25, etc. . In this case, 49 is a perfect square that is a factor of 98. This means we can rewrite the problem as the square root of 49 times the square root of 2. The square root of 49 is 7, so this simplifies to 7 times the square root of 2.
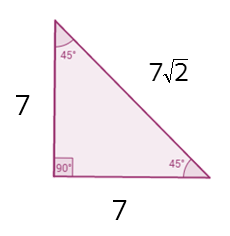
Now look back at the diagram. Do you see the shortcut? How is the length of the hypotenuse related to the length of the two legs?
Hopefully you can see that the hypotenuse is simply the length of one of the legs times the square root of 2. This happens every single time with a 45-45-90 triangle. So from now on, don't use the Pythagorean Theorem to find the hypotenuse. Use the shortcut and just multiply the leg by the square root of 2.