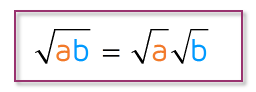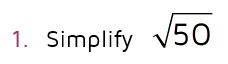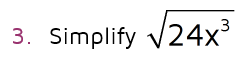|
|
The square root of 25 is just 5, so we can simplify the square root in the front. The second square root just has a 2 inside. 2 doesn't have any factors that are perfect squares other than 1, so that part we just leave as it is since it can't be simplified any more.
Think about the factors of 63. Start with the smallest perfect square and work your way up. Can you divide 63 by 4, 9, 16, 25, 36, 49, etc.? You can divide 63 by 9 and 9 is a perfect square. We can rewrite 63 as the product of 9 and 7 and split this problem up into two radicals.
7 doesn't have any factors that are perfect squares other than 1, so it's left under the radical sign.
You can also simplify radicals with variables under the square root. You'll want to split up the number part of the radicand just like you did before, but you'll also split up the variables too. With variables, you can only take the square root if there are an even number of them. If there's a variable to an odd exponent, you'll have a variable left over inside the radical.
Start with the 24. Do you know any factors of 24 that are perfect squares? 4 is a factor, so we can split up the 24 as a 4 and a 6. The 6 doesn't have any factors that are perfect squares so the 6 will be left under the radical in the answer.
Next look at the variable part. We can only take the square root of variables with an EVEN power (the square root of x squared, x to the 4th, x to the 6th, etc.) But we can split up the x cubed as x squared times x. Then we'll be able to take the square root of x squared and the single x leftover will go with the 6 inside the square root in the answer.
Practice
Ready to try simplifying some radicals on your own? Click the START button below to try a practice quiz.
|
Powered by Interact |