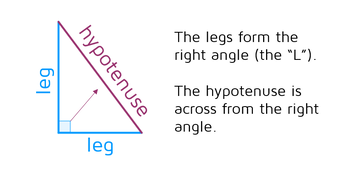
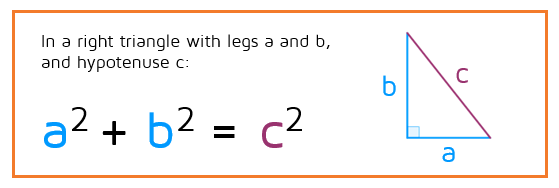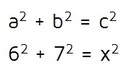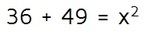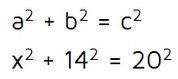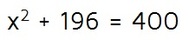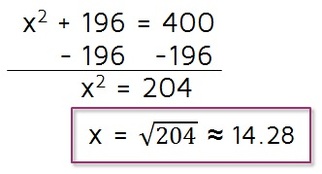Parts of a Right TriangleIn order to understand the Pythagorean Theorem, it's important that you know the different parts of a right triangle. The two sides that form the 90 degree angle are called the legs. These two sides are always the shortest two sides of the right triangle. The side that is across from the right angle is called the hypotenuse. The hypotenuse is always the longest side of the right triangle.
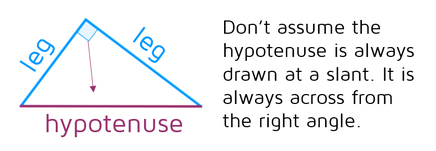
Want an easy way to remember which ones are the legs? If you trace them, they'll form the letter "L" for legs. If you have trouble figuring out which one is the hypotenuse, start at the square that marks the right angle and go across the triangle to the other side - that side will be the hypotenuse. A common mistake is for students to assume that the hypotenuse is always the one that's at a slant, but it just depends on how the triangle was drawn. You could easily rotate the picture and a different side could be slanted. Always look across from the 90 degree angle to find the hypotenuse.
|
|
How Do You Use the Pythagorean Theorem?
Why is the Pythagorean Theorem useful? If we know any two sides of a right triangle, it allows us to find the missing third side. You can use it if you're missing a leg or if you're missing the hypotenuse.
Step 1: Identify the values of a, b, and c.
Step 2: Plug a, b, and c into the Pythagorean Theorem.
Step 3: Simplify the equation.
Step 4: Solve for the missing value.
Step 1: Identify the values of a, b, and c.
Step 2: Plug a, b, and c into the Pythagorean Theorem.
Step 3: Simplify the equation.
Step 4: Solve for the missing value.
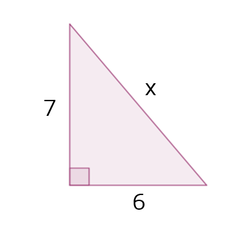
Example 1
Find x.
Step 1: Identify a, b, and c. The two sides that form the right angle are the legs a and b. We can see that the sides with lengths 6 and 7 form the letter "L" so they must be the legs. It doesn't matter which one is a and which one is b, you'll get the same answer either way.
a = 6
b = 7
The hypotenuse is across from the right angle. In this diagram, it's the missing side x.
c = x
Step 2: Plug the values into the Pythagorean Theorem.
Step 3: Simplify. Square each part and rewrite the equation.
Step 4: Solve for the missing value. The 36 and the 49 are on the same side of the equals sign, so we can add them together and rewrite it as an 85. To undo squaring a number, we take the square root of both sides. This means that x is the square root of 85, which is approximately equal to 9.22
Don't forget to check to make sure your answer is reasonable. Look back at the picture of the triangle we were given. Does it seem reasonable that the missing side would be 9.22? Yes. A common mistake students make is to forget to take the square root of both sides at the end. If we had said the answer was 85 on accident, we could catch our mistake by looking at the picture and realizing that that would be way too big for the missing side.
Example 2
Find x.
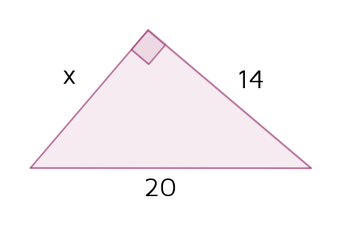
Step 1: Identify a, b, and c. The legs a and b form the right angle. The sides that form the letter "L" are the x and the 14, so they must be a an b. It doesn't matter which one is a and which one is b, you'll get the same answer either way. Let's say:
a = x
b = 14
The hypotenuse c is always across from the right angle. This means:
c = 20
A common mistake here is that students assume either the 14 or the x must be the hypotenuse since they're slanted. Remember, the diagram could be easily rotated around so any of the sides could be drawn at an angle. Always start at the square that marks the right angle and go across to the other side of the triangle to find the hypotenuse.
Step 2: Plug in the values of a, b, and c.
Step 2: Plug in the values of a, b, and c.
Step 3: Simplify.
Step 4: Solve.
The 196 and the 400 are not on the same side of the equals sign, so we can't add them together. We need to first get the x-squared term by itself on the left. To undo adding 196, we can subtract 196. Once we have the x-squared term by itself, we can take the square root of both sides to solve for x. This means x is equal to the square root of 204, which is approximately equal to 14.28.
Don't forget to look back at the triangle to make sure your answer seems reasonable. The missing side in this example is clearly one of the shorter sides so we should have expected our answer would be smaller than 20. A common mistake students might make on this problem would be to add the 196 and the 400 together instead of subtracting the 196 from both sides. This would give an answer of about 24.41, which is too large.
Pythagorean Theorem Video
Want to see another example? Check out the short video below.
Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.