30-60-90 Triangles                    Page 3 of 5

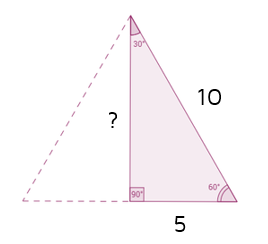
Long Leg of a 30-60-90 Triangle

We've figured out the relationship between the short leg and hypotenuse of a 30-60-90 triangle, but what about the longer leg? How do we find that one?  It's not quite as simple.  

The Long Way: Use the Pythagorean Theorem

There are two different ways to find the length of the long leg.  One way is to use the Pythagorean Theorem. In this example, we have a right triangle that's missing a side.  We can use the Pythagorean Theorem to find this missing side.

When you use the Pythagorean Theorem, it's important to label a, b, and c correctly.  a and b are the legs that form the right angle (they make an L shape). c must be the hypotenuse (the side across from the right angle).  In the triangle above, the 10 is the hypotenuse so we need to set c = 10.

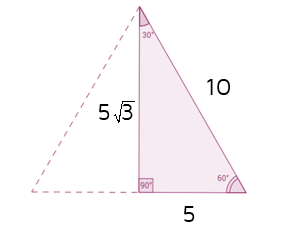
We could leave the answer for the hypotenuse as the square root of 75 or round it and get a decimal answer. To show the shortcut relationship, we can simplify the square root of 75 instead.  When you're simplifying a square root, look for factors of the number under the square root that are perfect squares.  See if you can divide the number by 4, 9, 16, 25, etc. .   

In this case, 25 is a perfect square that is a factor of 75. This means we can rewrite the problem as the square root of 25 times the square root of 3.  The square root of 25 is 5, so this simplifies to 5 times the square root of 3.

Now look at all three sides of the 30-60-90 triangle.  Do you see a shortcut you could use to find the long leg?

  1      2      ​3      4      5