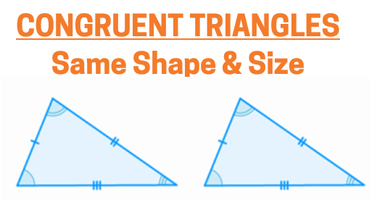
​Triangle Congruence Postulates                     Page 1 of 5
Accompanying Resources: 
​Printable Study Guide, Boom Cards, Activity for Google Drive

​
​What are Congruent Triangles?

Congruent triangles are triangles that are the exact same shape and size.  It's as if you put one in the copy machine and it spit out an identical copy to the one you already have.  One might be rotated or flipped over, but if you cut them both out you could line them up exactly. They have three sets of sides with the exact same length and three sets of angles that have the same degree measure.  

​Often the triangles' angles will be marked with different numbers of arcs to indicate which angles have the same degree.  In the diagram above, the angles marked with one arc each have the same angle measure, the angles with two arcs are matching and the angles marked with three arcs are matching.  The sides will often be drawn with little tic marks to indicate sets of congruent sides.  In the diagram above, the sides with one tic mark have the same length, the sides with two tic marks have the same length, and the sides with three tic marks have the same length.

How Do You Prove Two Triangles are Congruent?

There are several different postulates you can use to prove that two triangles are congruent - that they are exactly the same size and shape. The congruence postulates covered in this lesson are Side-Side-Side (SSS), Side-Angle-Side (SAS), Angle-Side-Angle (ASA), and Angle-Angle-Side (AAS).  There are more theorems that can be used to prove that right triangles are congruent, but the postulates in this lesson can be used for any type of triangle. Before we look at SSS, SAS, ASA, and AAS, we need to first talk about the word "included" - this is an important word to understand in order to make sense of the congruence postulates.

Welcome to Kate's Math Lessons!  

Teachers,make sure to check out the study guides and activities.

 1     2     3     4     5

Geometry teachers: Looking for resources to go with this lesson? Don't miss the Congruent Triangles Bundle.  There's a printable study guide, set of Boom Cards (digital, self-checking task cards), and an editable activity for Google Drive!