Triangle Congruence Postulates Page 4 of 5
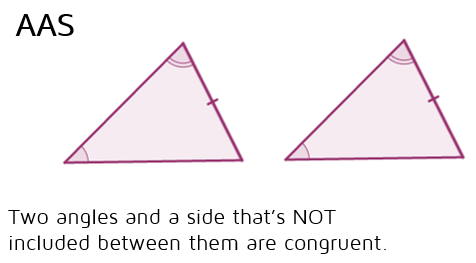
Angle-Angle-Side Postulate (AAS)
|
The AAS Postulate says that if two angles and the non-included side of one triangle are congruent to two angles and the non-included side of a second triangle, then the triangles are congruent. This is very similar to the ASA Postulate above because it also has two angles and a side. However, the big important difference between the two is where the side is located. In ASA, the side is in between the two angles on the triangle. In AAS, the S is listed at the end to indicate that the side is NOT in between the angles.
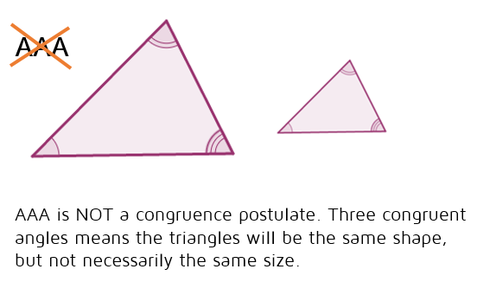
It doesn't matter which side is marked, as long as it's not the side that's between the two angles. In the diagram above, the bottom two sides could have been marked instead. What about AAA and SSA?Let's start with AAA - why isn't there an AAA Postulate? AAA would mean that you have triangles with 3 sets of congruent angles. Would these two triangles have to be exactly the same size and shape? Unfortunately not. We can draw two triangles with the exact same angles and make one larger than the other. They'll be the same shape, but not the same size. This means that AAA cannot be used to prove that triangles are congruent.
|
|