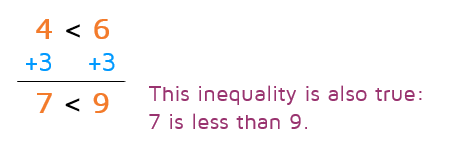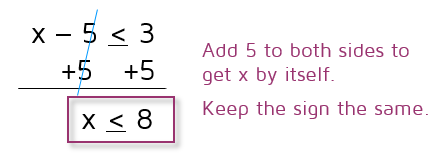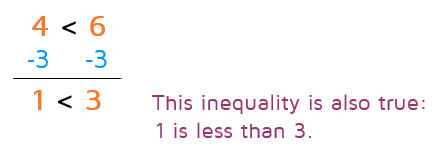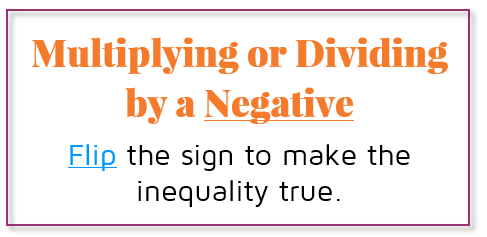When you're solving an equation with an = sign, you don't ever have to worry about the sign changing. But things are a little different if you're solving an inequality with <, >, <, or >, To solve the equation x - 2 = 5, you just add 2 to both sides. What happens if you change it to an inequality x - 2 < 5? Are the steps still the same?
Let's see by starting with an inequality that we know is true. We know that 4 is smaller than 6. We could write this as the inequality below. What happens if we add the same number to both sides of the equation? Will it still be a true inequality? If you add the same number to both sides of a true inequality, the new inequality will also be true. It basically just shifts everything over on the number line. If one side of the inequality was smaller than the other, it will still be smaller if you add the same number to both sides. In other words, you can add the same number to both sides of an inequality and the sign will stay the same. To solve the equation x - 2 = 6, you just add 2 to both sides. To solve the inequality x - 2 < 6, you follow the same exact steps and keep the sign the same. Here's an example: |
|
Using Subtraction to Solve an Inequality
What happens if you subtract the same number from both sides of an inequality? Let's see by starting with an inequality that we know is true: 4 < 6. What happens if we subtract 3 from both sides this time?
If you subtract the same number to both sides of a true inequality, the new inequality will also be true. It just shifts everything over the other direction on the number line. If one side of the inequality was smaller than the other, it will still be smaller if you subtract the same number from both sides.
In other words, you can subtract the same number from both sides of an inequality and the sign will stay the same. To solve the equation x + 2 = 7, you just subtract 2 from both sides. If we change it to the inequality x + 2 > 7, you follow the same exact steps and keep the sign the same.
Here's an example:
Multiplying or Dividing by a Positive to Solve an Inequality
Do the same rules apply when you're multiplying or dividing to solve an inequality? Let's start by looking at what happens if you multiply or divide an inequality by a positive number.
If you multiply or divide a true inequality by a positive number, the new inequality will also be true. You do not need to change the sign if you multiply or divide both sides by a positive number.
This means if you need to multiply or divide by a positive number to get a variable by itself, you just keep the inequality the same and solve the inequality just like you would solve an equation. Here's some examples:
Multiplying or Dividing by a Negative to Solve an Inequality
So far, we've been able to solve inequalities in the exact same way we solve an equation and just leave the inequality the same. The tricky part comes when you multiply or divide both sides of an inequality by a negative number.
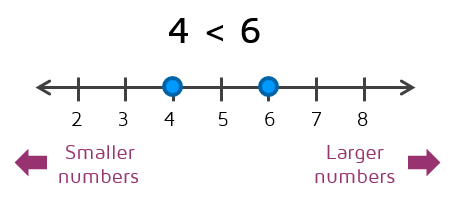
Let's start with the inequality that we know is true: 4 < 6. We know 4 is less than 6. Here's what this looks like on a number line.
Let's start with the inequality that we know is true: 4 < 6. We know 4 is less than 6. Here's what this looks like on a number line.
What happens if we multiply both sides of the inequality by a negative number?
If you multiply or divide both sides of an inequality by a negative number, the new inequality is no longer true! It basically flips things over on the number line, so the inequality from the original problem no longer applies to the new statement. How do we fix this problem? We flip the inequality sign. If we just reverse the inequality above from < to >, the statement becomes true.
If you're solving an inequality, you need to make sure to reverse the direction of the inequality sign if you multiply or divide both sides by a negative number. Here's an example:
Remember, you do not need to flip the sign if you're adding or subtracting. Don't be tempted to see a negative sign in the problem and assume you need to switch the sign. You only switch the sign if you have multiplied or divided both sides of the inequality by a negative number.
Practice Solving Inequalities
Ready to try solving some inequalities on your own? Click the START button below to try a practice quiz!
|
Powered by Interact |