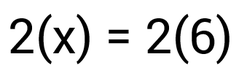​Logarithmic Equations with Logs on Both Sides       Page 1 of 4
​Accompanying Resource: Logarithmic Equations Boom Cards

Solving Equations with Logarithms 

Let's start with an equation without any logarithms:

​Do you know the answer?  2 times what number is the same as 2 times 6?

Option 1: You could simplify both sides first to get
2x = 12.  You can then divide both sides by 2 to get the x all by itself.

​Option 2: Can you look back and figure out the answer without doing much work?  

2 times some mystery number is the same as 2 times 6.  What must the mystery number be?  6.   When you have the same operation on each side, they essentially cancel each other out.

Welcome to Kate's Math Lessons!
​Teachers - don't miss the study guides and activities! 

  1      2      3      4