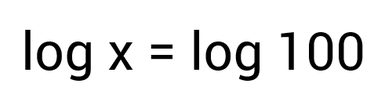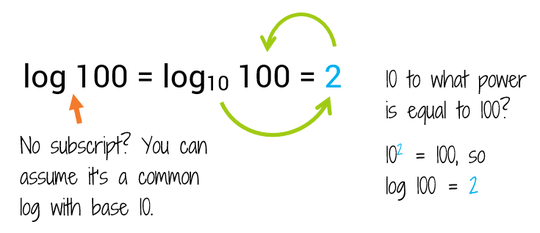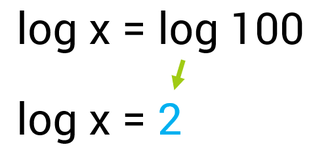Logarithmic Equations with Logs on Both Sides Page 2 of 4
|
Now let's try an equation with logarithms: Don't let this scare you off just because you see logarithms. If you're thinking "What is a logarithm?!?" you might want to check out the intro to logarithms lesson before moving forward. Option 1: Let's start by examining the logarithm on the right side of the equation, the log 100. There's no small number written after the word log, so we can assume that it's a common logarithm with base 10. Remember, a logarithm tells you what the exponent is. So log 100 really means "10 to what power is equal to 100?" We know 10 to the 2nd power is 100, so the logarithm is equal to 2. |
|
Now that we know the right side of the equation is just 2, we can rewrite the equation.
Now you're left with an equation with only one logarithm. Since there's no subscript after the word log, we know it's a common log with base 10. We can rewrite this as an exponential equation and see that the answer is 100.
But that's a whole lot of unnecessary work! Instead, you can just look at the original equation and see that x and 100 must be the same thing. If you have the same operation on both sides of an equation, they cancel each other out!
Keep in mind that this only works when the logarithms on both sides of the equation have the same base. If you had a logarithm with base 3 on one side and a logarithm with base 7 on the other side, they won't cancel out.