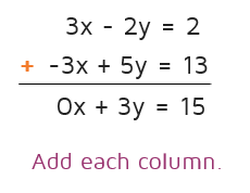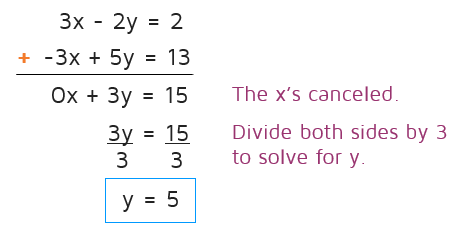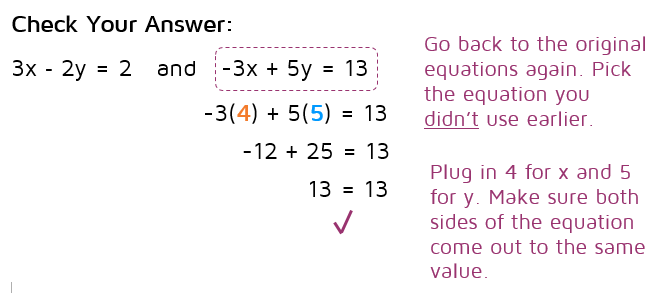Elimination Method (Level 1) Page 3 of 3
Example 2Solve the system: 3x - 2y = 2 and -3x + 5y = 13
Step 1: Add the equations vertically. First, rewrite one equation right below the other. Make sure the variables, equal signs, and constants are lined up. 
After you get everything lined up, add straight down. 
|
|
Did you notice what happened? This time the x's canceled out. The goal with the elimination method is to always get one of the variables to cancel, it doesn't matter which one. 0x is the same as 0, so we can rewrite the equation without it.
Step 2: Solve for the first variable.
Now that the x's are gone, you can solve the equation for y.
Step 3: Solve for the second variable.
Now that you have one variable, we need to plug it in one of the original equations to find the other variable. Pick the original equation that looks the easiest, you'll get the same answer no matter which one you choose. We'll choose the first equation and plug in 5 for y.
Pay careful attention to where you plug the value in! Make sure you put the 5 in for the y-value.
Step 4: Write answer as an ordered pair.
Now that you know both x and y, put them together to write your answer as an ordered pair. Make sure to write them in alphabetical order: x goes first, y goes second.
Step 5: Check your answer.
It's pretty easy to check your answer when using the elimination method. We used the first equation to solve for x, so we need to check our answer in the second equation. If you use the same equation twice, you won't catch a mistake if there is one.
If we had plugged in x and y and it came out to a number other than 13, we would know to go back and look for a mistake along the way.
Elimination Method Video
Check out the short video below to see an example of solving a system of equations with the elimination method.
Practice
Ready to solve some systems on your own? Click the START button below to try a practice quiz on the elimination method.
Powered by Interact
