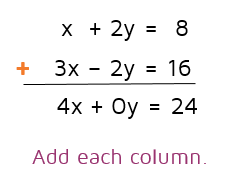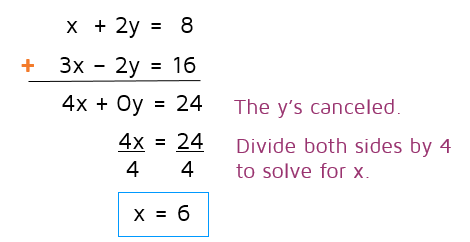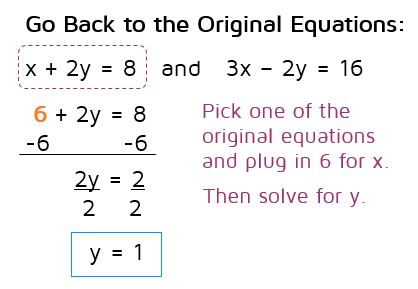Elimination Method (Level 1) Page 2 of 3
|
|
Did you notice what happened? We "eliminated" the y's. They canceled out.
Step 2: Solve for the first variable.
Now that the y's are gone, we can solve the equation for x.
We're half-way! A common mistake is for students to get one variable and stop there. Remember, the solution to a system is an ordered pair that works for both equations so we need the x and y values to write the answer.
Step 3: Solve for the second variable.
Now that we know one variable, plug it back in one of the original equations to find the other variable. Pick which ever equation looks easiest to you.
Step 4: Write answer as ordered pair.
Now that we know x and y, we can write our final answer as an ordered pair. Remember to always write them in alphabetical order. If your variables are x and y, you always write the x first.
Step 5: Check your answer.
You can check your answer by plugging the x and y values back into one of the original equations. Make sure to use the equation that you didn't use before. If you use the same original equation twice, it won't catch a mistake if there is one. We used the first equation: x + 2y = 8 to solve for y, so we'll use the second equation: 3x - 2y = 16 to check our answer. Plug in 6 for x and 1 for y and make sure it comes out to 16.
If we had plugged in the values for x and y and it came out to 10 or something instead of 16, that would tell us there's an error somewhere along the way. The most common mistakes are sign errors, so always start by looking back to see if you dropped a negative along the way. Another common error is to copy the original equations down wrong, so it doesn't hurt to check to make sure you copied the problem correctly too.