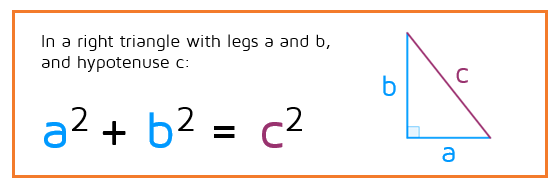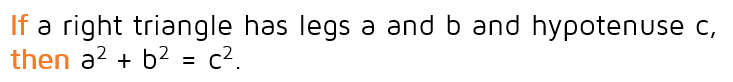Converse of the Pythagorean Theorem

The Pythagorean Theorem

Before we get to the converse, let's do a quick review of the Pythagorean Theorem. Make sure to check out the full lesson on the Pythagorean Theorem if this isn't review for you.

We can use the Pythagorean Theorem to find the missing side of a right triangle. If you know two of the sides of a right triangle, you can plug them in and solve to find the missing third side.

The important thing to notice here is that in order to use the Pythagorean Theorem, you have to first know for certain that the triangle has a 90 degree angle. You could reword the theorem this way:

You can reword the Pythagorean Theorem as an if-then statement. If a right triangle has legs a and b and hypotenuse c, then a-squared plus b-squared equals c-squared.

The order is very important! You can use the Pythagorean theorem only if you start out knowing that the triangle is a right triangle. Only then can you use a-squared plus b-squared equals c-squared to find a missing side.

Notice the order of the Pythagorean Theorem. You must know you have a right triangle in order to use it.

Why does this matter? Let's see what happens if you switch the order around.

The Converse of the
Pythagorean Theorem

If you're familiar with if-then statements, you may remember that the converse of a statement is when you switch the hypothesis and conclusion around (the parts after if and then).

To write the converse of a statement, you switch the hypothesis (p) and conclusion (q) around.

Welcome to Kate's Math Lessons!

Teachers: make sure to check out the study guides and activities.

$Picture$

Notice that the order has been switched! In the Pythagorean Theorem, the hypothesis (the part after the "If") is that it's a right triangle with legs a and b and hypothesis c. The conclusion (the part after the "then") is that a-squared plus b-squared equals c-squared. The converse is written in the reverse order.

The converse of the Pythagorean Theorem can be written as an if-then statement by switching the hypothesis and conclusion of the original theorem.

Notice that the order is switched around. In the original Pythagorean Theorem, you know from the start that the triangle is a right triangle and then you can use a-squared plus b-squared equals c-squared to find a missing side. In the converse, you start by knowing that a-squared plus b-squared equals c-squared, and then you can tell that it's a right triangle.

The order is switched around in the converse of the Pythagorean Theorem. You start by knowing that a-squared plus b-squared equals c-squared and then know that the triangle must be a right triangle.

If you already know that the triangle is a right triangle, you can use the original Pythagorean Theorem to find a missing side. The converse is used the other way around. If you know all three sides of a triangle, you can use the converse of the Pythagorean Theorem to determine if the triangle is a right triangle.

When you're using the converse, you will already know all three sides of the triangle and you'll be asked if the triangle is a right triangle. If it is a right triangle, the longest side would be the hypotenuse so you'll choose the largest number for c. The smaller two numbers will be a and b, it doesn't matter which one you call a and which one you call b. You plug all three numbers into a-squared plus b-squared equals c-squared and see if it works! If both sides of the equation come out to the same number, then you know the triangle is a right triangle. If they come out to different numbers, you know that it's not a right triangle.

Steps to Using the Converse of the
Pythagorean Theorem

In this type of problem, you'll be given the three sides of a triangle and you need to figure out if it's a right triangle. How do you know if it is a right triangle? You use the converse of the Pythagorean Theorem. Here are the steps you'll follow:

How do you use the converse of the Pythagorean Theorem to determine if a triangle is a right triangle?

Example 1

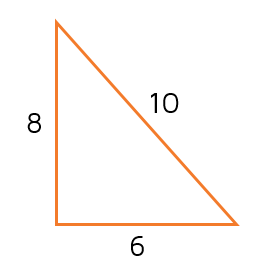
Determine if the triangle below is a right triangle.

Example of the converse of the Pythagorean Theorem.

This sure looks like a right triangle, but never just assume a triangle has a 90 degree angle by just looking at it. It may have a 89 degree angle or a 91 degree angle and just look awfully close to 90 degrees. We need to use the converse of the Pythagorean Theorem to tell for sure if it has a right angle.

Step 1: Determine a, b, and c. If this was a right triangle, the longest side would be the hypotenuse, so we need to use 10 for c. The two shortest sides 6 and 8 will be the values for a and b.

Step 2: Plug in a, b and c.

How do you use the converse of the Pythagorean Theorem to tell if a triangle is a right triangle?

Step 3: Determine if the sides form a right triangle. Both sides of the equation simplified to 100. When both sides come out to the same number, it works! A triangle with sides 6, 8, and 10 do form a right triangle.

Example 2

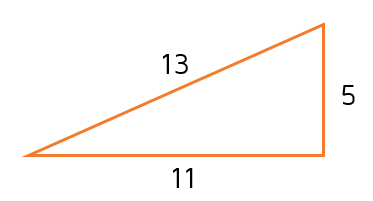
Determine if the triangle below is a right triangle.

How do you tell if a triangle is a right triangle?

Again, don't assume this is a right triangle just because it looks like one. To verify if a triangle is a right triangle, we need to use the converse of the Pythagorean Theorem to make sure.

Step 1: Use the longest side for c: c = 13. The two shorter sides are a and b.
Step 2: Plug in the values and see if they work.

How to use the converse of the Pythagorean Theorem to figure out if a triangle is a right triangle.

Step 3: Determine if the triangle is a right triangle. The two sides of the equation simplified to different numbers. This means the conditions of the converse were not met, so the triangle is not a right triangle.

Practice

Ready to try some problems on your own? Click the START button below to take a practice quiz.