Comparing and Ordering Integers Activities
What are Integers?
Did you know there are different types of numbers? For example, the numbers 0, 1, 2, 3 . . . are called whole numbers.
Integers are similar to whole numbers, but also include negative numbers. There are an infinite number of integers, so it's impossible to list them all out for you but I've listed some below. Integers do not include decimals or fractions.
Integers: . . . -3, -2, -1, 0, 1, 2, 3 . . .
Examples of Integers: 8, -42, 153, -6
NOT Integers: 1/2, -7.3, π, √5
Another way to describe the set of integers is to say they are the set of positive whole numbers, their opposites, and zero.
Want to learn more about integers and other types of numbers? Check out my classifying real numbers lesson.
Integers are similar to whole numbers, but also include negative numbers. There are an infinite number of integers, so it's impossible to list them all out for you but I've listed some below. Integers do not include decimals or fractions.
Integers: . . . -3, -2, -1, 0, 1, 2, 3 . . .
Examples of Integers: 8, -42, 153, -6
NOT Integers: 1/2, -7.3, π, √5
Another way to describe the set of integers is to say they are the set of positive whole numbers, their opposites, and zero.
Want to learn more about integers and other types of numbers? Check out my classifying real numbers lesson.
How Do You Compare Integers?
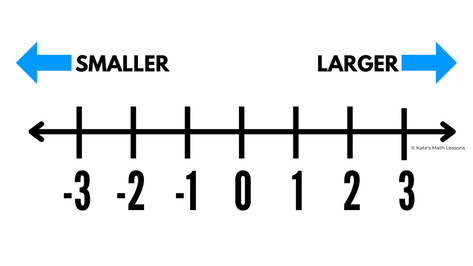
To compare integers, it really helps to look at them in order on a number line. As you move to the left on a number line, the numbers get smaller. As you move to the right on a number line, the numbers get larger.
You can use a number line to compare two integers. The integer that is furthest to the right will be the larger integer and the integer that is furthest to the left will be the smaller integer.
For example, let's say you're comparing the integers 1 and 3. We can see that 1 is to the left of 3. This means that 1 is the smaller integer. You can write this as 1 < 3 (you read this as 1 is less than 3). You could also say that 3 is to the right of 1, so 3 is the larger number and write it the other way around as 3 > 1 (you read this as 3 is greater than 1).
For example, let's say you're comparing the integers 1 and 3. We can see that 1 is to the left of 3. This means that 1 is the smaller integer. You can write this as 1 < 3 (you read this as 1 is less than 3). You could also say that 3 is to the right of 1, so 3 is the larger number and write it the other way around as 3 > 1 (you read this as 3 is greater than 1).
Comparing Integers Examples
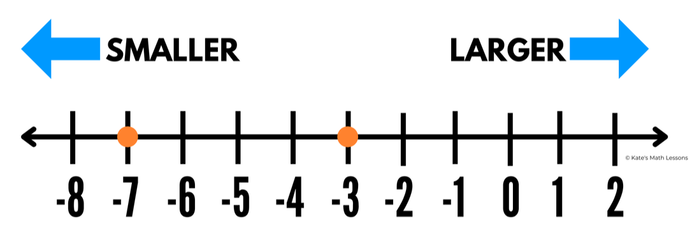
1) Write an inequality to compare the integers -7 and -3.
To compare two integers, it helps to see where they are on a number line. Remember, as you move to the left on a number line the numbers are getting smaller. As you move to the right on a number line, the numbers are getting larger. This will help you figure out which integer is smaller and which is larger.
Take a look at -7 and -3 on a number line:
To compare two integers, it helps to see where they are on a number line. Remember, as you move to the left on a number line the numbers are getting smaller. As you move to the right on a number line, the numbers are getting larger. This will help you figure out which integer is smaller and which is larger.
Take a look at -7 and -3 on a number line:
-7 is to the left of -3 on the number line. This means that -7 is smaller than -3. You can write this as -7 < -3 (you read this as -7 is less than -3).
Another way to compare these would be to say that -3 is the larger integer because it's to the right of -7. You can write this as -3 > -7 (you read this as -3 is greater than -7).
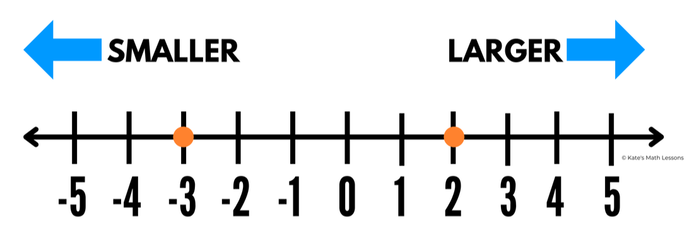
2) Write an inequality to compare the integers -3 and 2.
To compare these integers, take a look at where they are in relation to each other on a number line. Which integer is smaller? Which integer is larger?
Another way to compare these would be to say that -3 is the larger integer because it's to the right of -7. You can write this as -3 > -7 (you read this as -3 is greater than -7).
2) Write an inequality to compare the integers -3 and 2.
To compare these integers, take a look at where they are in relation to each other on a number line. Which integer is smaller? Which integer is larger?
We can see that -3 is to the left of 2. This means that -3 is smaller than 2. We can write this as -3 < 2 (you read this as -3 is less than 2).
Another way to compare them would be to say that 2 is larger than -3 since it's to the right. We can write it this way as 2 > -3 (you read this as 2 is greater than -3).
Another way to compare them would be to say that 2 is larger than -3 since it's to the right. We can write it this way as 2 > -3 (you read this as 2 is greater than -3).
Rules to Compare and Order Integers
Students sometimes ask me "What are the rules to compare and order integers?" My simple answer is that you shouldn't try to memorize rules for comparing or ordering integers. Instead of trying to remember a list of rules, it's much easier to draw a quick number line to help you compare and order positive and negative integers.
The more you use a number line, the more you'll notice some of the patterns or "rules" that are below. Don't try to memorize these, instead read them and make sure they make sense to you based on how a number line works.
Positive numbers are always larger than negative numbers.
If you're comparing two integers with different signs, the positive one will always be the greatest. You can use a number line to remember this because all of the positive integers are to the right on a number line and all the negative numbers are to the left.
Any time you're comparing integers with different signs, the positive one will always be the largest. For example, if you're comparing -8 and 3, we automatically know -8 < 3 because -8 is negative and 3 is positive.
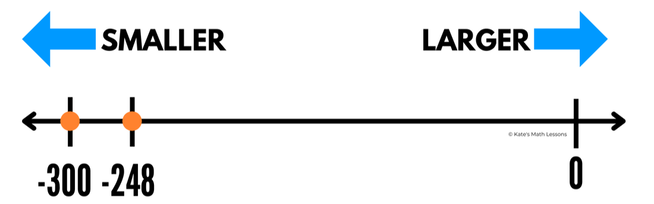
When comparing two negative numbers, look at the absolute value of the numbers to help you. By absolute value, I mean the distance the number is from 0 on a number line (this is the same number you'd get if you just take off the minus sign). For example, let's say you're comparing -248 and -300. The absolute value of -248 is 248. This means it's 248 units to the left of 0 on a number line. The absolute value of -300 is 300. This means it's 300 units to the left of 0 on a number line.
-300 is farther to the left of 0 on a number line, so it's the smaller of the two integers. You can write this as -300 < -248 (you read this as -300 is less than -248).
Again, don't try to memorize this rule. This is hopefully something you'll start to notice on your own the more you practice comparing integers.
The more you use a number line, the more you'll notice some of the patterns or "rules" that are below. Don't try to memorize these, instead read them and make sure they make sense to you based on how a number line works.
Positive numbers are always larger than negative numbers.
If you're comparing two integers with different signs, the positive one will always be the greatest. You can use a number line to remember this because all of the positive integers are to the right on a number line and all the negative numbers are to the left.
Any time you're comparing integers with different signs, the positive one will always be the largest. For example, if you're comparing -8 and 3, we automatically know -8 < 3 because -8 is negative and 3 is positive.
When comparing two negative numbers, look at the absolute value of the numbers to help you. By absolute value, I mean the distance the number is from 0 on a number line (this is the same number you'd get if you just take off the minus sign). For example, let's say you're comparing -248 and -300. The absolute value of -248 is 248. This means it's 248 units to the left of 0 on a number line. The absolute value of -300 is 300. This means it's 300 units to the left of 0 on a number line.
-300 is farther to the left of 0 on a number line, so it's the smaller of the two integers. You can write this as -300 < -248 (you read this as -300 is less than -248).
Again, don't try to memorize this rule. This is hopefully something you'll start to notice on your own the more you practice comparing integers.
If you're not sure about your answer when you're comparing integers, it always helps to at least draw out a rough number line to help you think about the problem. Your number lines don't have to be perfect or even include every number. The goal is to use a number line to figure out which integer will be further to the left and which one will be further to the right.
How to Order Integers
Sometimes you'll be given a list of several integers and you'll be asked to write them in order from least to greatest (or maybe greatest to least).
To put integers in order, it also can help to see where they all are on a number line. Then you'll want to write them in order from left to right if you're asked to put them in ascending order from least to greatest.
If you're asked to write them the other way around (in descending order from greatest to least), you'll list them in order from right to left. Pay careful attention to which order the question gives you!
To put integers in order, it also can help to see where they all are on a number line. Then you'll want to write them in order from left to right if you're asked to put them in ascending order from least to greatest.
If you're asked to write them the other way around (in descending order from greatest to least), you'll list them in order from right to left. Pay careful attention to which order the question gives you!
Ordering Integers Examples
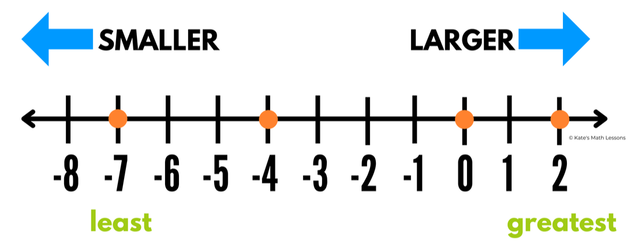
1) Write the numbers -4, 2, -7 and 0 from least to greatest.
To order these integers, it will help to see where they are on a number line. Always remember that smaller numbers are to the left on a number line and larger numbers are to the right.
To put these integers in order, we can plot them on a number line to help us.
To order these integers, it will help to see where they are on a number line. Always remember that smaller numbers are to the left on a number line and larger numbers are to the right.
To put these integers in order, we can plot them on a number line to help us.
The question asked us to order them from least to greatest. This means we need to list the smallest integer first. To list integers in ascending order (from least to greatest), start on the left side of the number line and list them in order from left to right. -7 is the farthest to the left, so it's the smallest. As we move from left to right, we get to -4 next, then 0, and 2 is the greatest.
One way to write your answer is to just list the numbers in order from smallest to largest.
ANSWER: -7, -4, 0, 2
Another way to write this is to use inequality signs to indicate that they're written from least to greatest.
ALTERNATE ANSWER: -7 < -4 < 0 < 2
You can read this as "-7 is less than -4, which is less than 0, which is less than 2."
One way to write your answer is to just list the numbers in order from smallest to largest.
ANSWER: -7, -4, 0, 2
Another way to write this is to use inequality signs to indicate that they're written from least to greatest.
ALTERNATE ANSWER: -7 < -4 < 0 < 2
You can read this as "-7 is less than -4, which is less than 0, which is less than 2."
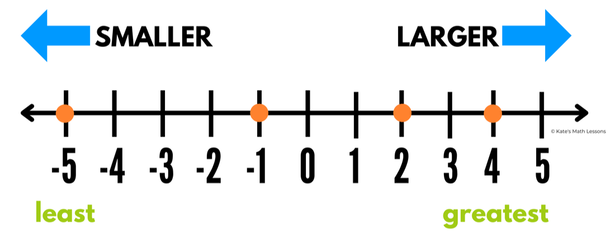
2) Write the numbers 2, -1, -5 and 4 from greatest to least.
To find the answer, it will help if we plot the integers on a number line. In this question, we need to put them in order from largest to smallest, so this time we'll start on the right side of the number line and work our way to the left side.
To find the answer, it will help if we plot the integers on a number line. In this question, we need to put them in order from largest to smallest, so this time we'll start on the right side of the number line and work our way to the left side.
We can see on the number line that 4 is the largest so we'll start with that first and then list them in order from right to left. You can list them in order or use greater than signs to show that you've written them in descending order from largest to smallest.
ANSWER: 4, 2, -1, -5
ALTERNATE ANSWER: 4 > 2 > -1 > -5
You can read the second answer as "4 is greater than 2, which is greater than -1, which is great than -5."
ANSWER: 4, 2, -1, -5
ALTERNATE ANSWER: 4 > 2 > -1 > -5
You can read the second answer as "4 is greater than 2, which is greater than -1, which is great than -5."
Comparing and Ordering Integers Practice Activity
Need some extra practice to help you or your students order and compare integers with and without a number line?
Don't miss these digital, self-grading activities:
Comparing and Ordering Integers Boom Cards (digital task cards)
Compare and Order Integers Digital Activity for Google
Pin the image below so you'll remember this math lesson later.
Don't miss these digital, self-grading activities:
Comparing and Ordering Integers Boom Cards (digital task cards)
Compare and Order Integers Digital Activity for Google
Pin the image below so you'll remember this math lesson later.