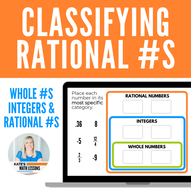
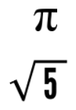Ready to learn about whole numbers, integers, and rational numbers? Scroll down to the first green heading. If you also want to learn about natural numbers, irrational numbers, and real numbers, you'll want to skip to my Classifying Real Numbers lesson instead.
|
Accompanying Resource:
Classifying Rational Numbers Boom Cards |
Types of Numbers
|
Did you know that numbers haven't been around forever? Way back when, people didn't have words or symbols for numbers as simple as 1, 2, 3. . . Before numbers and their symbols were invented, people used sticks and made tally marks on stones as ways to keep track of things. Thankfully, a number system developed over time so we no longer need to use sticks or hold up fingers to count! We now have names and symbols that we use to represent numbers. (Want to see some of the earlier symbols that were used? Check out this article on the history of the number system.)
|
The number system that we use today has different types of numbers. In this lesson, we'll look at 3 types: whole numbers, integers, and rational numbers.
Whole Numbers
0, 1, 2, 3 . . .
The whole numbers start at zero and count up. I think of these as the numbers you learn when you're young. They do not include negative numbers, fractions, or decimals.
Examples of Whole Numbers:
5
23
167
14
NOT Whole Numbers:
8.9
-2
3/5
Bonus Note: Did you know people had a really hard time accepting 0 as a number? They used to think it was crazy to have a number represent "nothing." I hope you're glad it was invented, because we wouldn't have computers without the number 0! Check out this history of the number zero to learn more interesting facts about 0 (did you know some thought it was evil?).
The whole numbers start at zero and count up. I think of these as the numbers you learn when you're young. They do not include negative numbers, fractions, or decimals.
Examples of Whole Numbers:
5
23
167
14
NOT Whole Numbers:
8.9
-2
3/5
Bonus Note: Did you know people had a really hard time accepting 0 as a number? They used to think it was crazy to have a number represent "nothing." I hope you're glad it was invented, because we wouldn't have computers without the number 0! Check out this history of the number zero to learn more interesting facts about 0 (did you know some thought it was evil?).
Integers
. . . -3, -2, -1, 0, 1, 2, 3 . . .
This set of numbers is similar to the whole numbers, but also includes negative numbers. Integers do not include fractions or decimals. All of the whole numbers are also integers.
Examples of Integers:
8
-34
721
-5
NOT Integers:
6.2
-7/8
This set of numbers is similar to the whole numbers, but also includes negative numbers. Integers do not include fractions or decimals. All of the whole numbers are also integers.
Examples of Integers:
8
-34
721
-5
NOT Integers:
6.2
-7/8
Rational Numbers
Numbers that can be written as a fraction.
Any number that can be expressed as a fraction is considered to be a rational number. I would list them out for you, but that's impossible because there are so many! All of the integers are also rational numbers because you can rewrite any of them as a fraction using a 1 in the denominator (for example, 5 can be rewritten as the fraction 5/1). Rational numbers also include terminating decimals (decimals that stop at some point), repeating decimals (like .2323. . . ), and numbers that are already written as fractions.
Examples of Rational Numbers:
13.25
-7 (This can be written as the fraction -7/1)
2/5
.4444 . . . . (This can be written as the fraction 4/9)
NOT Rational Numbers:
A decimal that goes on forever without ending or repeating is not rational. Here are two examples:
Any number that can be expressed as a fraction is considered to be a rational number. I would list them out for you, but that's impossible because there are so many! All of the integers are also rational numbers because you can rewrite any of them as a fraction using a 1 in the denominator (for example, 5 can be rewritten as the fraction 5/1). Rational numbers also include terminating decimals (decimals that stop at some point), repeating decimals (like .2323. . . ), and numbers that are already written as fractions.
Examples of Rational Numbers:
13.25
-7 (This can be written as the fraction -7/1)
2/5
.4444 . . . . (This can be written as the fraction 4/9)
NOT Rational Numbers:
A decimal that goes on forever without ending or repeating is not rational. Here are two examples:
Using Graphic Organizers to Classify Rational Numbers
|
Here's a graphic organizer to help you understand how these three types of numbers are related to each other. The whole numbers are inside of the integers in the diagram because all of the whole numbers are also integers. The integers are inside of the rational numbers in the diagram because all of the integers are also rational numbers.
|
Let's say you have to classify the following numbers:
-10
8.2
23
When I classify numbers, I find it helpful to start with the innermost section (the most specific type) and work my way out. Let's start with the -10. Is -10 a whole number? No. Whole numbers start at 0 and do not include negative numbers so it's not a whole number. Is -10 an integer? Yes. The integers include -1, -2, -3, -4, etc. so -10 is an integer.
Note that -10 is also a rational number since it can be written as a fraction (-10/1). This is similar to how a square is also a rectangle, but the term square is more specific. The term integer is more specific than rational number.
How about 8.2? Is it a whole number? No, whole numbers do not included decimals. Is it an integer? No, integers do not include decimals either. Is it a rational number (can it be written as a fraction)? Yes, it's a terminating decimal (a decimal that stops) so it can be written as a fraction. 8.2 can be written as the fraction 82/10. This means 8.2 is a rational number.
How about 23? Is it a whole number? Yes, the whole numbers include 0, 1, 2, 3, 4 . . . . so 23 is a whole number. This means that it is also an integer and it is also a rational number, but the most specific term to use for the number 23 in this case is to say it's a whole number.
Teachers: Don't miss the accompanying Classifying Rational Numbers self-checking activity.
Looking to learn about more types of numbers? Learn about natural numbers and irrational numbers in my Classifying Real Numbers lesson.
-10
8.2
23
When I classify numbers, I find it helpful to start with the innermost section (the most specific type) and work my way out. Let's start with the -10. Is -10 a whole number? No. Whole numbers start at 0 and do not include negative numbers so it's not a whole number. Is -10 an integer? Yes. The integers include -1, -2, -3, -4, etc. so -10 is an integer.
Note that -10 is also a rational number since it can be written as a fraction (-10/1). This is similar to how a square is also a rectangle, but the term square is more specific. The term integer is more specific than rational number.
How about 8.2? Is it a whole number? No, whole numbers do not included decimals. Is it an integer? No, integers do not include decimals either. Is it a rational number (can it be written as a fraction)? Yes, it's a terminating decimal (a decimal that stops) so it can be written as a fraction. 8.2 can be written as the fraction 82/10. This means 8.2 is a rational number.
How about 23? Is it a whole number? Yes, the whole numbers include 0, 1, 2, 3, 4 . . . . so 23 is a whole number. This means that it is also an integer and it is also a rational number, but the most specific term to use for the number 23 in this case is to say it's a whole number.
Teachers: Don't miss the accompanying Classifying Rational Numbers self-checking activity.
Looking to learn about more types of numbers? Learn about natural numbers and irrational numbers in my Classifying Real Numbers lesson.