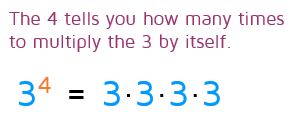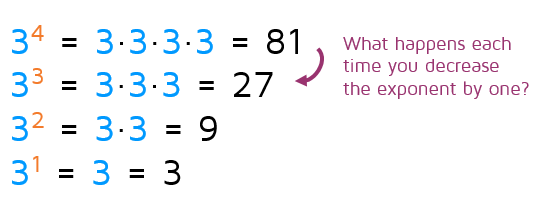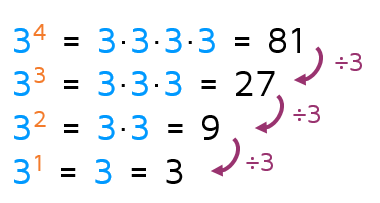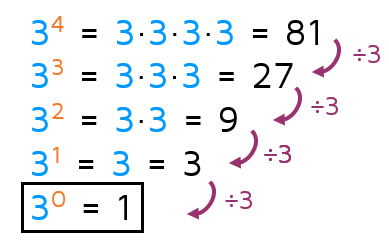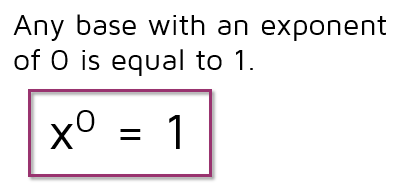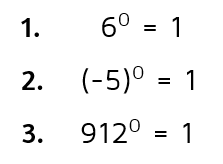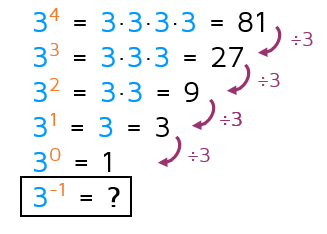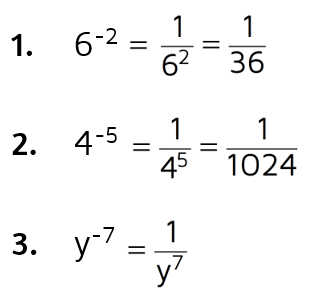Zero and Negative Exponents

Note: This lesson includes zero and negative exponents. For a full lesson with all the exponent rules (Product Rule, Quotient Rule, Power Rule, Power of a Product Rule, etc.), make sure to see my full Exponent Rules Course.

Accompanying Resources:
Writing Expressions Using Exponents Boom Cards,
Evaluating Exponents Boom Cards

$Writing Expressions with Exponents Boom Cards - digital activity great for distance learning!$

Evaluating Exponents Boom Cards - digital activity great for distance learning!

What is an Exponent?

You have probably used positive exponents before. A positive exponent (often called a power) tells you how many times to multiply a number by itself. For example, 3 to the 4th power means 3 times itself 4 times.

A positive exponent tells you how many times to multiply the base by itself.

It gets a little tricker if the exponent is zero or negative. Let's start by looking for a pattern. We'll start with 3 to the 4th power and decrease the exponent by one each time. What do you notice?

As the exponent decreases, what happens to the result?

If you said the answer is getting smaller, you're right. Can you be more specific? What could you do with the 81 to get 27? What could you do with the 27 to get 9? What could you do with the 9 to get 3? You can divide by 3.

So what happens if the exponent goes down to 0? We can just extend the pattern and divide by 3 again.

When you divide by 3 one more time, all the 3's have now canceled out! There are "zero 3's" left. When you have a 0 as the exponent, it cancels everything out and there's only a 1 left over.

Welcome to Kate's Math Lessons!

Teachers: make sure to check out the study guides and activities.

$Picture$

A Zero Exponent

Any number to the zero power is equal to 1. When the exponent is 0, you can think of it as "zero 3's" or zero of whatever the base is. Everything has canceled out and there is only a 1 left over.

Any base with an exponent of 0 is equal to 1.

Examples

The list could go on and on. It doesn't matter what the base is. Any number to the 0 power is equal to 1.

Negative Exponents

Let's look back at the pattern we examined in the first tab. What happens if we continue this pattern and make the exponent a -1?

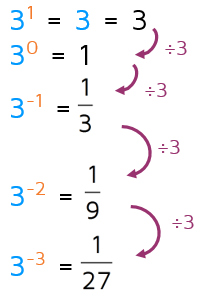
Every time we reduce the exponent by one, we can divide by 3 to find the new result. If we continue this pattern when the exponent is -1, we need to divide by 3 one more time. This gives us the fraction 1/3. We can continue the pattern to see additional negative exponents. As we divide by 3 more and more, the fraction gets smaller and smaller.

The basic idea is that a negative exponent tells you how many times to divide by the base. This means we can rewrite any expression with a negative exponent as a division problem.

An expression with a negative exponent can be rewritten as a division problem.

When you rewrite the expression, make sure to use a positive exponent in the denominator.

Examples

Simplifying expression with negative exponents.

Practice

Ready to try a few problems on your own? Click the START button below to try a practice quiz. If you want to learn more about exponents, make sure to see my Exponents Course to learn how to use the product rule, quotient rule, power rule, etc. to simplify expressions with exponents.