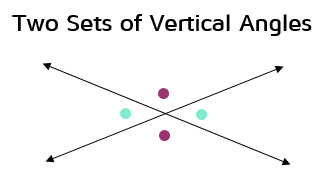
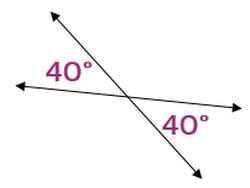
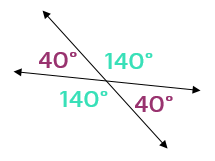
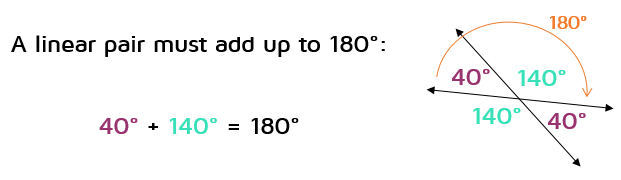Vertical Angles                       Page 1 of 3
​Accompanying Resources:  Printable Study Guide, Vertical Angles Activity

What are Vertical Angles?

When two lines cross, they form 4 angles. The angles that are across from each other are called vertical angles. Intersecting lines always form two sets of vertical angles:

​Using Vertical Angles

Vertical angles are always congruent - they always have the same angle measure.  If one angle is 40 degrees, the vertical angle across from it will also be 40 degrees.

What about the other two angles in the diagram above that aren't labeled?  We can use what we know about vertical angles to help us find those angle measures as well.  We know that a full circle is always 360 degrees, so if we added all 4 angles together they must add up to 360 degrees.  The two 40 degree angles add up to 80 degrees, which means the missing two must add up to 360 - 80 = 280.  Since they are also vertical, they must be the same angle measure.  So we can simply divide 280 by 2 to figure out each one:  280/2 = 140.  This means the missing two angles must be 140 degrees.

Welcome to Kate's Math Lessons!  

Teachers: make sure to check out the study guides and activities.

There's another way we could have figured out that the missing two angles were 140 degrees. The intersecting lines form sets of linear pairs - angles that are right next to each other that form a straight line.  We know that a straight line is always 180 degrees (it's half way around a circle), so we also could use the fact that any two angles right next to each other in the diagram above must also add up to 180 degrees.  

You can use what you know about vertical angles and linear pairs to find missing angles formed by intersecting lines.

                                                                                    1      2      3