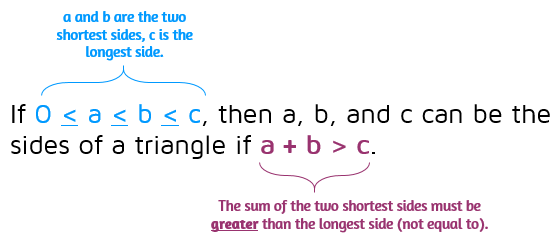|
|
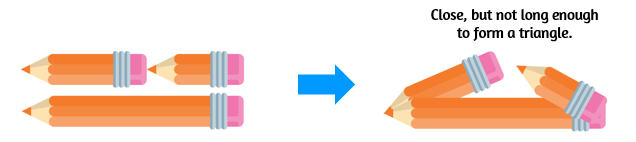
What if you put the two short ones end to end and they're exactly the length of the longest side? In order to "bump out" to form a triangle, there has to be a little extra room. If they're just barely touching the ends of the longest side when they're parallel to the longest side, there's no room for them to angle out and form a triangle. The two shortest sides put end to end must be longer than the longest side. If you tried to put the two shortest ones at an angle, they would be very close to forming a triangle, but not quite long enough.
The Triangle Inequality Theorem
The Triangle Inequality Theorem is just a more formal way to describe what we just discovered. We found that when you put the two short sides end to end (that's the sum of the two shortest sides), they must be longer than the longest side (that's why there's a greater than sign in the theorem).
This is just one way to state the Triangle Inequality Theorem. Another way to state it is to say that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side.
Here's the important thing to remember:
Short side + Short side > Longest Side
If you put the two shortest sides end to end, they have to be longer than the longest side to be able to angle up to form a triangle.
Example 1
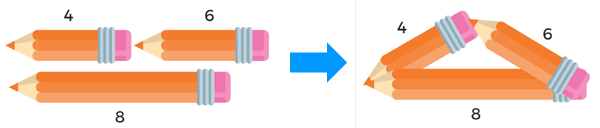
Determine if the given side lengths can form a triangle: 4, 6, and 8.
First, identify the two shortest sides: 4 and 6. If you find the sum of the two shortest sides, is it greater than the longest side?
First, identify the two shortest sides: 4 and 6. If you find the sum of the two shortest sides, is it greater than the longest side?
There's a visual of this below. If you put the two shortest sides end to end, they will be longer than the longest side. This means they're long enough to reach when you angle them out to form a triangle.
Example 2
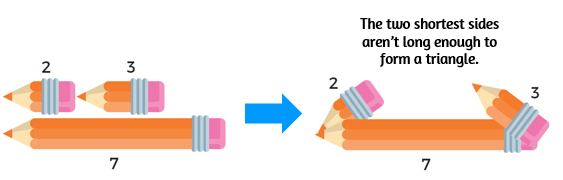
Determine if the given side lengths can form a triangle: 7, 3, and 2.
First, identify the two shortest sides: 3 and 2. If you find the sum of the two shortest sides, is it greater than the longest side?
First, identify the two shortest sides: 3 and 2. If you find the sum of the two shortest sides, is it greater than the longest side?
There's a visual of this below. If you place the two shortest sides end to end, they aren't long enough to be placed at an angle to form a triangle.
Example 3
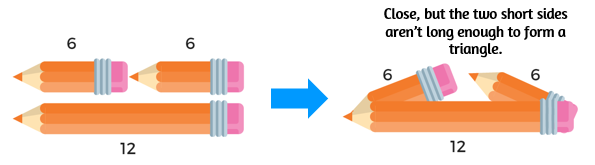
Determine if the given side lengths can form a triangle: 6, 6, and 12.
First, identify the shortest two sides: 6 and 6. Is the sum of the two shortest sides greater than the longest side? In this case 6 + 6 is exactly 12. Does it work when the sum is exactly the same as the longest side?
First, identify the shortest two sides: 6 and 6. Is the sum of the two shortest sides greater than the longest side? In this case 6 + 6 is exactly 12. Does it work when the sum is exactly the same as the longest side?
No, it does not work when the two shortest sides add up to the exact same length as the longest side. The sum must be larger (not equal to) the longest side. If it's exactly the same, there's no room to for the shorter two sides to angle up to form a triangle.
Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.