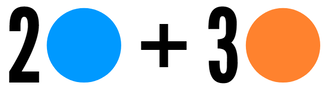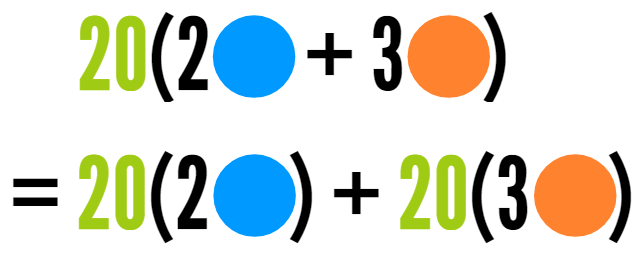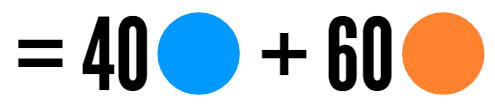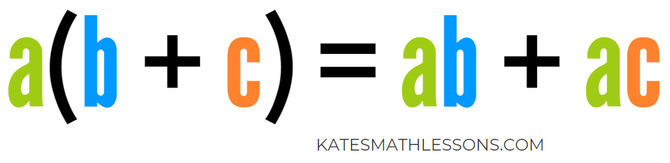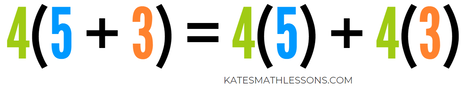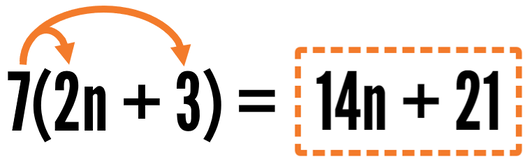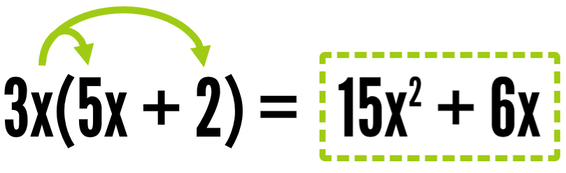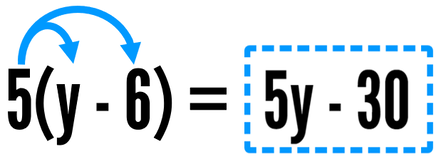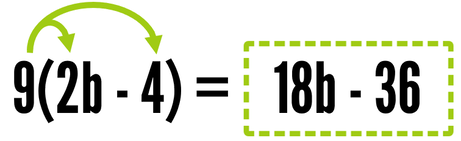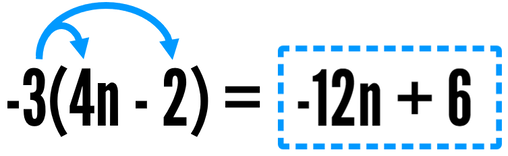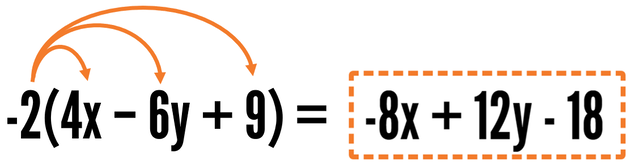How Does the Distributive Property Work?Before we go over the distributive property, let's first look at an example. Let's say an art teacher is doing a project that requires each student to have 2 blue circles of paper and 3 orange circles. We could represent this with the picture below:
So now let's say a class is coming in and there are 20 students in the class. How many blue circles will she need? How many orange circles will she need? She could set out 20 individual sets of 2 blue circles and 3 orange circles to make sure she has enough. But I'm guessing you figured it out a faster way! You get the same answer if you multiply each part by 20. |
|
Either way, you get the same answer. You can add what's in the parentheses 20 times. Or you can take the shortcut and multiply the 20 by each term in the parentheses.
The Distributive Property
Don't let the variables in the distributive property confuse you! We'll look at some examples to help you understand what it means. Here's what the Distributive Property says:
To simplify an expression with parentheses, you can distribute the a on the outside to the b and the c on the inside. You multiply each term on the inside of the parentheses by the term on the outside. Let's look at an example with numbers instead of variables to help you understand the property.
The distributive property says we can take the 4 that's being multiplied on the outside of the parentheses and distribute it to the 5 and the 3 on the inside. Do you believe this statement is true? If we simplify the left side, we would add 5 + 3 first and get 4(8), which is 32. If we simplify the right side, we would multiply 4(5) and get 20 and multiply 4(3) and get 12. 20 + 12 = 32. Both sides are equal to the same number!
Here's an example with a variable: 6(x + 2) To simplify this expression with the distributive property, we can distribute the 6 to each term inside the parentheses. We do this by multiplying the x and the 2 by 6. Then simplify each term to write the final answer.
Here's an example with a variable: 6(x + 2) To simplify this expression with the distributive property, we can distribute the 6 to each term inside the parentheses. We do this by multiplying the x and the 2 by 6. Then simplify each term to write the final answer.
When you're writing these out by hand, it will probably take too long to color coordinate the terms like I did above. A faster way to show your work when you're distributing is to use arrows like in the example below to show that you're distributing the 6.
Distributive Property Examples
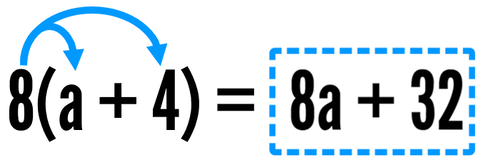
Here are a few more examples to help you understand how the distributive property works.
We can simplify 8(a + 4) by multiplying the a and the 4 by 8. 8 times a is 8a and 8 times 4 is 32.
We can simplify 7(2n+3) by multiplying each term inside the parentheses by 7. 7 times 2n is 14n and 7 times 3 is 21.
This example is a little harder because we have to multiply each term on the inside by a term with a variable. 3x times 5x is 15 x squared (Remember, x times itself is x to the second power). 3x times 2 is 6x.
Distributive Property with Minus Signs
You can also use the distributive property if the expression on the inside of the parentheses has a minus sign instead of a plus sign.
You will sometimes even see the Distributive Property written like this: a(b - c) = ab - ac
Subtracting is just adding the opposite, so the rule works for addition and subtraction. In the example above, you can think of it as 5 times y and 5 times negative 6. 5 times -6 is -30 so your answer will have a minus sign between the terms.
Here's another example with a minus sign between the terms. 9 times 2b is 18b and 9 times -4 is -36.
Don't assume that if there's a minus sign in the parentheses, that your answer will have a minus sign! You need to be careful with the signs when multiplying. In this example, you're multiplying the inside terms by a negative 3. Negative 3 times negative 2 is a positive 6, so the final answer has a plus sign.
Distributive Property with 3 or More Terms
Know what to do if there's 3 or more terms on the inside of the parentheses? Just keep multiplying until you've multiplied the outside term by each term on the inside. If there are 3 terms on the inside, you'll have to multiply 3 times. If there are 4 terms, multiply 4 times, etc.
In the example above, you need to multiply -2 by each term on the inside. -2(4x) = -8x, -2(-6y) = 12y Notice that a negative times a negative is a positive! Be careful with your signs when you're simplifying. Last, -2(9) = -18. When you multiply and the term ends up negative, make sure to put a minus sign in your simplified answer.