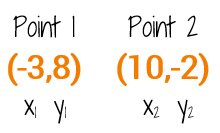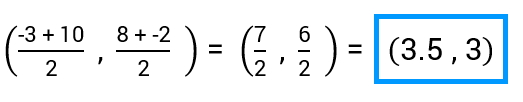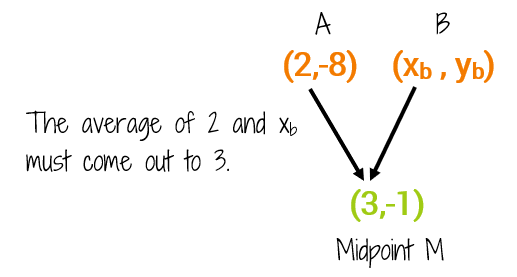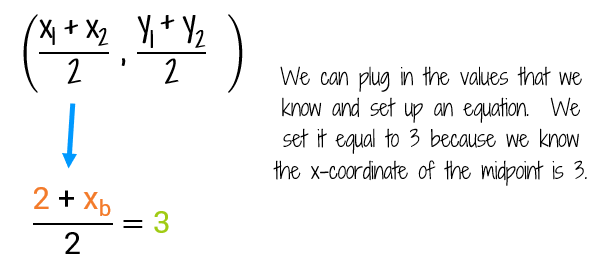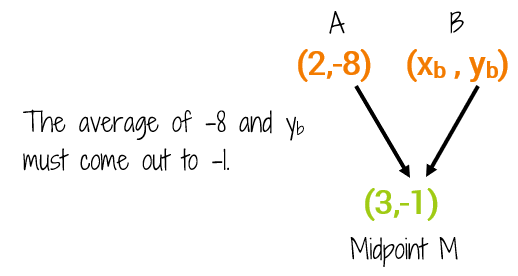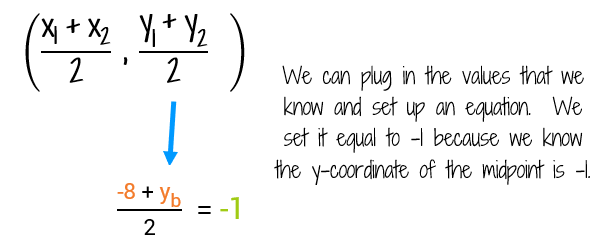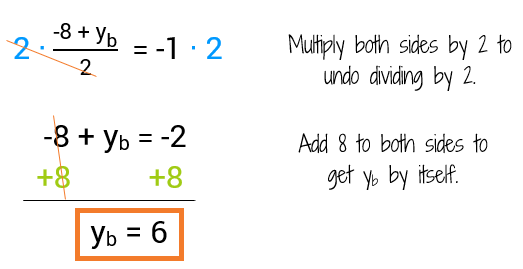Accompanying Resources: 
Midpoint Formula Google Drive Activity (FREE!)
Midpoint Formula Boom Cards (digital task cards)

​I'll Meet You Halfway

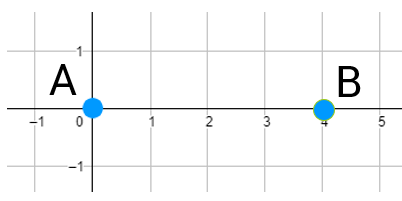
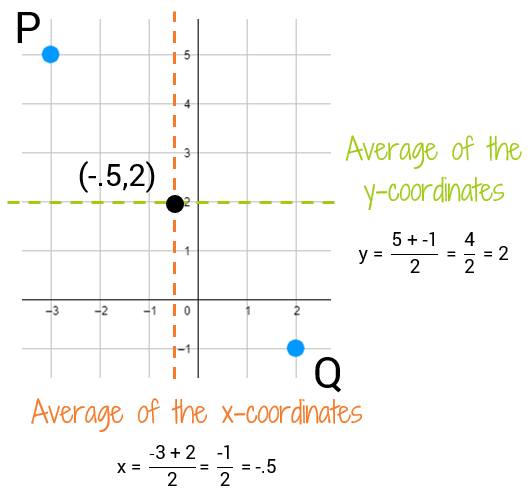
The midpoint of two points is the point that's exactly halfway between them.  How do you find the midpoint? Let's look at an example and see if we can figure it out.

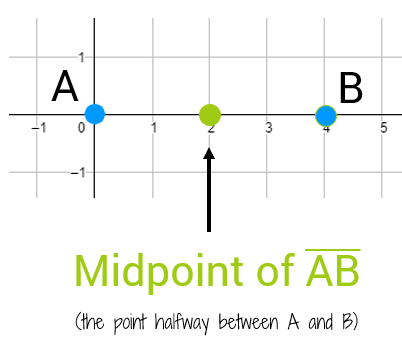
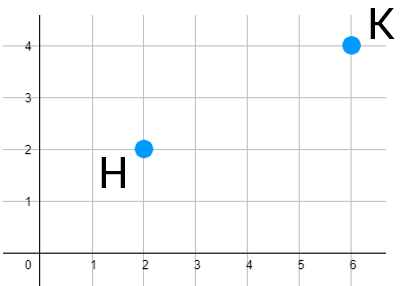
Let's say you're standing at Point A and I'm standing at Point B.  If I say I'll meet you halfway, where will I meet you?

There's a total of 4 spaces between us, so if we divide it exactly in half that means we each need to walk 2 spaces toward the middle.  This puts the midpoint at (2,0).

Ok, so maybe that example was too obvious.  Let's look at a different example.  Now let's say you're at the point C and I'm at D.  Where is the midpoint between these two points?

This time there are 4 spaces between, so we would each have to split the difference and move 2 spaces towards the middle.  This puts the midpoint at (0,3).

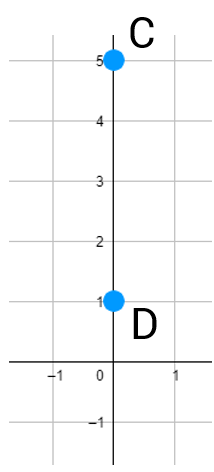
Ok, so that one was maybe a little obvious as well.  To make it harder, let's say you didn't have graph paper and I just gave you the coordinates.  Now can you find the midpoint?  

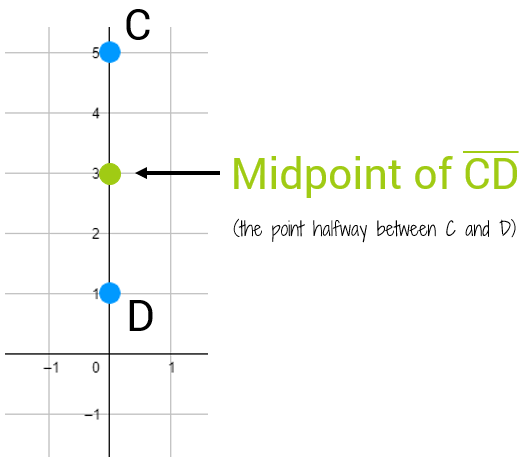
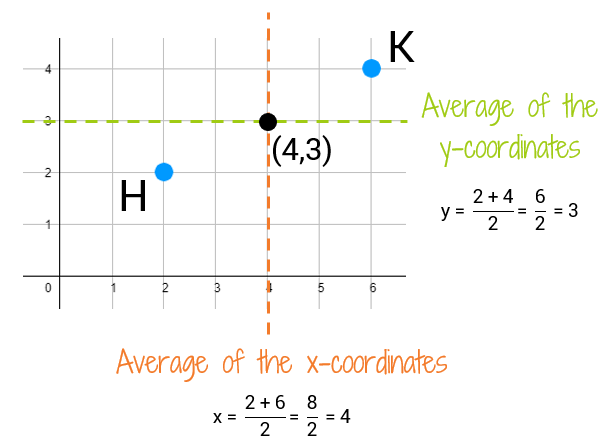
How could you have found the midpoints of the two different line segments without using a graph?  Could you still figure it out?  In the last example, we had the points C(0,5) and D(0,1).  Since both endpoints have an x-coordinate of 0, it makes sense that the midpoint also has an x-coordinate of 0.  But what about the 3?  3 is just the average of 5 and 1 (to find the average of two numbers, you add them together and divide by 2:  (5 + 1)/2 = 6/2 = 3).   

This will work even if your two points aren't on the same horizontal or vertical line.  To find the midpoint, you simply find the average of the x-coordinates and find the average of the y-coordinates.  This will give you the location of the point that's exactly halfway between the two points.

​Example 1

Let's say you have points H(2,2) and K(6,4).  Can you find the midpoint between H and K?

To find the midpoint, we need to find the average of the x-coordinates and the average of the y-coordinates.  This will give us the coordinates of the point smack dab in the middle.

The average of the x-coordinates is 4 and the average of the y-coordinates is 3.  This means the midpoint is at the point (4,3).

​Example 2

Find the midpoint between the points P(-3,5) and Q(2,-1).

We do the same thing as before.  Find the average of the x-coordinates and find the average of the y-coordinates.  Just make sure to be extra careful when adding positive and negative numbers together! 

The average of the x-coordinates is -1/2, or -.5.  The average of the y-coordinates is 2.  This means the midpoint is at (-.5,2).  

The Midpoint Formula

The Midpoint Formula is just a more formal way to write down the steps that we took above.  Here's the official formula (or at least a version of it):

Don't let all the little subscripts scare you away!  This is just a fancy way of showing that you need to average the x-coordinates and average the y-coordinates.  It's just saying to add the two x-coordinates together and divide by 2, then add the two y-coordinates together and divide by 2.  Don't stress about which point is Point 1 or Point 2.  You'll get the same answer no matter which point you decide to call Point 1.

Example 3

Find the midpoint between the points (-3,8) and (10,-2).

If it helps, you may want to label the points first.  Remember that the x-coordinates are always listed first in an ordered pair.  It doesn't matter which one you call Point 1 or Point 2.  You can switch them around and you'll still get the same answer.

Next, plug the values into the formula.  Remember, you're finding the average of the x-coordinates and the average of the y-coordinates.

Welcome to Kate's Math Lessons!  

Teachers,make sure to check out the study guides and activities.

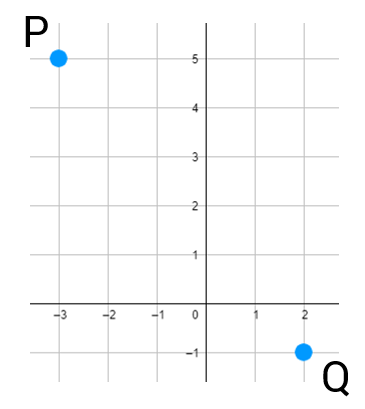
It's not required, but it's a good idea to make a quick sketch of the points to see if your answer for the midpoint is reasonable (or at least try to visualize it in your head).  It's easy to make mistakes when you're adding negative numbers (How do you add negative numbers?), so a rough sketch can often help you catch a mistake.

The point (3.5,3) looks like it's right in the middle to me!
​

Finding a Missing Endpoint

If you're studying the Midpoint Formula in your math class, chances are you'll run into some problems that ask you to find the missing endpoint of a segment given one endpoint and the midpoint.  These types of problems are a little trickier, so let's take a look at an example.

Example 

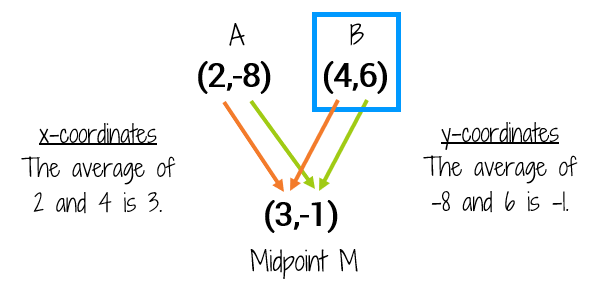
M(3,-1) is the midpoint between points A(2,-8) and B.  Find the coordinates of B.

You could get out graph paper and try to sketch out the segment to see where B would lay.  Or you can use the Midpoint Formula and work your way backwards!  Let's start with the x-coordinates.  We know that if we take the two endpoints of a segment and average their x-coordinates, we get the x-coordinate of the midpoint.  This means the average of 2 and some number must be 3.  We'll label the coordinates of B with a small subscript b.

If we know the average of 2 and the x-coordinate of B must come out to 3, we can write this as an equation.  When we do this step, we're using the first half of the Midpoint Formula.  

Do you know how to solve this equation?  One way is to think about the steps that you normally take to find the midpoint and go in reverse.  Normally you add the two x-coordinates together first and then divide by 2.  If you go backwards, you need to use inverse operations to undo those steps.  To undo dividing both sides by 2, we need to multiply both sides by 2 first.  (Another option is to make the right side of the equation into a fraction by putting a 1 in the denominator.  Then you can cross-multiply.  Both options end up with the same answer.)

We found that the x-coordinate of the missing endpoint must be 4.  We can double check this pretty easily.  Does the average of 2 and 4 equal 3?  (2 + 4)/2 = 6/2 = 3.

If you do this type of problem enough, you may start to be able to visualize it without needing to set up an equation.  You can practice this with graph paper or try to picture in your head how far apart the points have to be.

Don't forget about the y-coordinate! We're going to repeat the process, this time with the y-coordinates.  We know the y-coordinate of A is -8 and the y-coordinate of the midpoint M is -1.  This tells us that the average of -8 and some number must come out to -1.

We can use the second half of the Midpoint Formula to set up another equation to find the missing y-coordinate.

Now all we need to do is work our way backwards to solve for the missing y-coordinate.  To undo dividing by 2, we multiply both sides by 2.  Then instead of subtracting -8 from both sides, we'll add a positive 8 to make it easier.

Let's double check it quick.  Is the average of -8 and 6 equal to -1?  (-8 + 6)/2 = -2/2 = -1.  Yes!

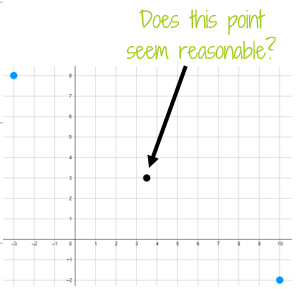
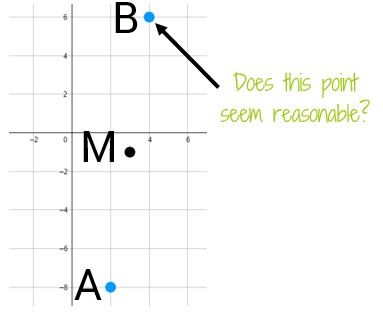
It's not a bad idea to sketch a graph after you find your answer to see if it looks reasonable.  It doesn't need to be a detailed exact graph, a rough sketch can at least help you make sure you're in the right area!   

​Does (4,6) seem like a reasonable spot for B? It sure looks like M is halfway between A and B to me! 


Need help with the Distance Formula? There's a free lesson for that too!