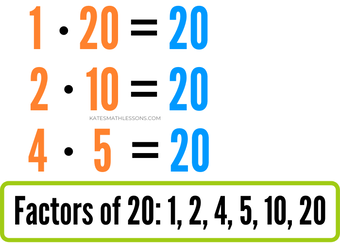Accompanying Resources: GCF Digital Activity for Google Sheets, GCF Digital Activity for Google Forms, GCF Task Cards (printable & digital options)
Review: What are Factors?
|
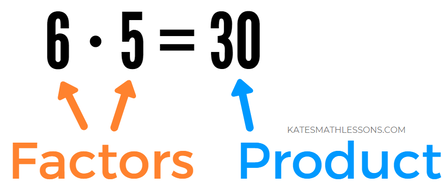
Before you can find a greatest common factor, let's make sure you understand what a factor is. If you're brand new to this term, make sure to check out my full Factors and Multiples lesson for more examples. Factors are whole numbers that can be multiplied together to equal a product.
For example, 6 and 5 are both factors of 30 because 5 times 6 is equal to 30. |
An integer that's greater than 1 will always have at least two factors: 1 and itself. Many numbers have several factors. For example, the number 20 has six different factors.
Need help finding the factors of a number? Make sure to check out the examples in my Factors and Multiples lesson.
What is a Greatest Common Factor (GCF)?
A Greatest Common Factor (commonly referred to as a GCF) is the largest number that is a factor of two or more numbers. It's the biggest number that will divide evenly into the numbers given.
For example, the Greatest Common Factor of 8 and 12 is 4. 8 and 12 both have several factors, but the largest factor that they both have in common is 4. This also means that 4 is the largest number that will divide evenly into 8 and 12.
For example, the Greatest Common Factor of 8 and 12 is 4. 8 and 12 both have several factors, but the largest factor that they both have in common is 4. This also means that 4 is the largest number that will divide evenly into 8 and 12.
How to Find a GCF
There are TWO different methods you can use to find a greatest common factor in math. You can choose the method that seems easiest or fastest to you. Both methods will result in the same answer, so it doesn't really matter which option you choose.
Method 1: List the factors of each number to find the GCF.
One way to find a GCF is to make a list of the factors of each number. Then look at each list and find the largest number that they have in common.
For example, let's look at how to find the GCF of 12 and 18. First, start by making a list of the factors of 12 and the factors of 18.
For example, let's look at how to find the GCF of 12 and 18. First, start by making a list of the factors of 12 and the factors of 18.
After you've made a list of each number, look for the largest number they have in common as a factor. This number is the greatest common factor. It's the biggest number that is a factor of both 12 and 18.
I always start at the largest factor of one of the numbers and work my way down. In this example, I would start with the 12 at the end of the first list. Is there a 12 listed as a factor of 18? No. 12 is only a factor of the first number, not both.
Next I look at the next largest factor of 12: the 6. Is 6 also a factor of 18? Yes! 6 is the largest number that's a factor of both 12 and 18. This means that the GCF of 12 and 18 is 6.
I always start at the largest factor of one of the numbers and work my way down. In this example, I would start with the 12 at the end of the first list. Is there a 12 listed as a factor of 18? No. 12 is only a factor of the first number, not both.
Next I look at the next largest factor of 12: the 6. Is 6 also a factor of 18? Yes! 6 is the largest number that's a factor of both 12 and 18. This means that the GCF of 12 and 18 is 6.
Method 2: Using Prime Factorization to Find a GCF
If the numbers you're working with are large, it can take a long time to list out all the factors. Another way to find a GCF is to use their common prime factors. An easy way to get the prime factors of a number is to use a factor tree!
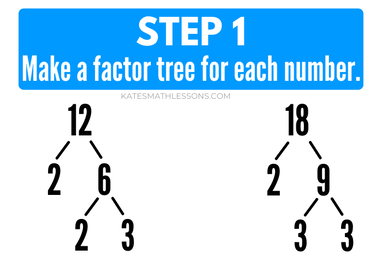
For example, let's look at how to find the GCF of 12 and 18 with the prime factorization method. The first step is to find the prime factors of each number. We can find these by making a factor tree for both 12 and 18.
For example, let's look at how to find the GCF of 12 and 18 with the prime factorization method. The first step is to find the prime factors of each number. We can find these by making a factor tree for both 12 and 18.
The next step is to look at your factor trees and make a list of the prime factors of each number. If a number is repeated as a factor, make sure to list all of them.
Next, you want to see which prime factors they have in common and circle these numbers. In this example, they both have prime factors of 2 and 3 in common.
The last step is to multiply the common prime factors together. This will give you the GCF. The common prime factors are 2 and 3, so we multiply them together and get 6 as the GCF (which is the same answer we got with the other method!).
You can choose either method, whichever one seems easiest to you. If the numbers are small, I typically use the first method of listing out the factors. If the numbers are larger or I know they have a lot of factors, I'll usually use the second method and make factor trees to find the prime factors. Both methods will give the same answer.
Another GCF Example
Here's one more example of how to find a greatest common factor with both methods. This time we'll look at the GCF of 30 and 45. You can use the first method and list out all the factors of both numbers and look for the largest factor that they have in common. In this case, 15 is the largest factor that both numbers have in common. Or you can use the second method and use factor trees to find all the prime factors, then multiply the common prime factors together. They both have prime factors of 3 and 5, you multiply these together to get 15 as the GCF.
Finding a GCF of 3 or More Numbers
Sometimes you'll be asked to find the greatest common factor of 3 or more numbers. Don't worry! It's the same process to find the GCF, just with more numbers. If you choose the first method, make sure to find the largest factor that all the numbers have in common.
The example below shows how to find the GCF of three numbers: 30, 45, and 20. It's just like the example from earlier, except this time you need to find the factor that all three numbers have in common. If you choose the second method, make sure to only multiply the prime factors that they all have in common. In this case, they only have one prime factor in common so the GCF is 5.
The example below shows how to find the GCF of three numbers: 30, 45, and 20. It's just like the example from earlier, except this time you need to find the factor that all three numbers have in common. If you choose the second method, make sure to only multiply the prime factors that they all have in common. In this case, they only have one prime factor in common so the GCF is 5.