The Discriminant            Page 3 of 4

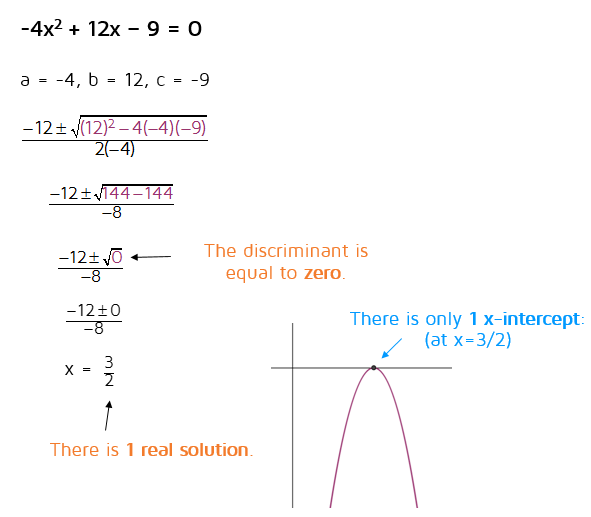
When the Discriminant is Zero

If the discriminant is 0, that means you have a 0 under the square root in the quadratic formula.  What happens when you have a 0 under a square root?  The square root of 0 is just 0.  When this happens, the plus or minus part of the quadratic formula essentially just goes away. This will leave you with only 1 real solution.

If there's only one real solution, that means that the graph will only have 1 x-intercept.  The parabola will hit the x-axis right at its maximum or minimum point.  

​Here's an example of a quadratic equation with a discriminant of 0:

A Negative Discriminant

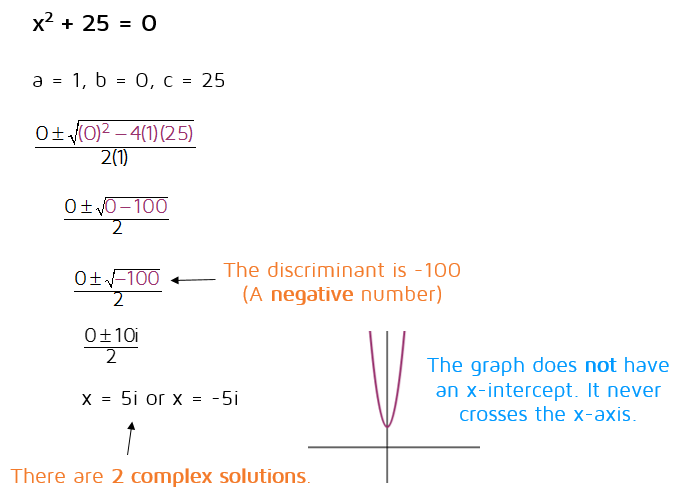
If the discriminant is negative, that means there is a negative number under the square root in the quadratic formula.  You may have learned in the past that you "can't take the square root of a negative number."  The truth is that you can take the square root of a negative number, but the answer is not real.  The square root of a negative number will involve the imaginary number i.  This means that if you have a negative discriminant, you will get two complex solutions.  

If the solutions are both complex, you will not see them on the graph.  The graph will either be too high or too low and will not cross the x-axis.  There will be not be any x-intercepts.

​Here's an example of a quadratic equation with a negative discriminant:

 1      2      ​3     4