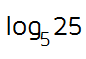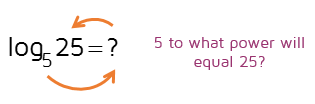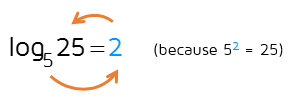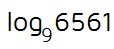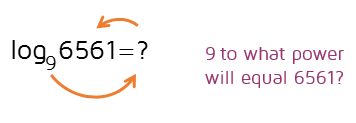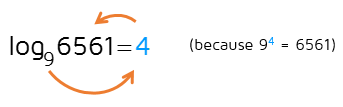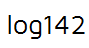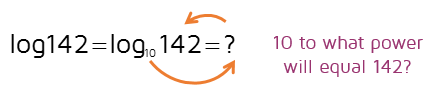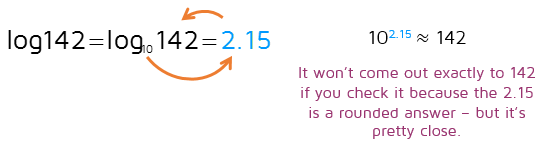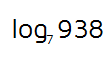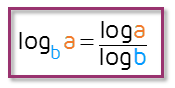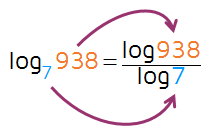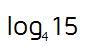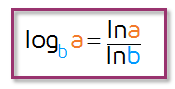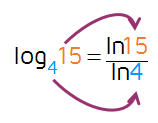|
|
Don't know the answer off the top of your head? You're not alone. Start trying some numbers. How about 9 squared? 9 to the 3rd power?
4 is the exponent that works. Since 9 to the 4th power is equal to 6561, this means the logarithm is equal to 4.
Decimal Logarithms
The two logarithms we looked at above both came out to whole numbers. Does this always happen? Unfortunately not. Take a look at the logarithm below.
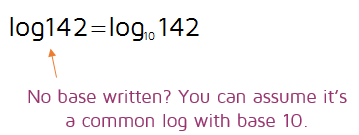
Always start by identifying the base of a logarithm. In this problem, there's no little number written after the word log. This means it's a common log - a logarithm with base 10.
So now we have a log base 10 of 142. This means 10 to what power will equal 142?
Well, it's not 2. 10 squared is 100. And it's not 3. 10 to the third power is 1,000. So in order for this to come out to 142, the exponent is going to have to be somewhere in between 2 and 3.
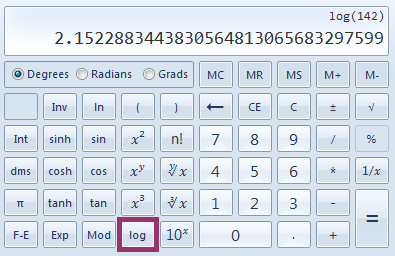
You could guess and check all day trying to figure out the decimal between 2 and 3 that makes this work. Thankfully, most calculators are programmed to deal with common logarithms. Look for the "log" button on your calculator. If it just says log with no little number after it, you can assume it's for common logarithms - logs with base 10. So we can just type in log 142 and it gives us the answer!
There are lots of different calculators out there, so the logarithm button may be in a different place on your calculator. Ask a teacher for help if you're not able to find yours. When you type in log142 on a calculator, it will show you the answer above: 2.152288. . . . We knew the answer would be between 2 and 3 so that's a good sign! When a logarithm is a decimal, you can usually round to one or two numbers after the decimal so we would say the answer is approximately 2.15. This means that 10 to the (approximately) 2.15 power equals 142.
The Change of Base Formula
So if your calculator has a log button, can't you always just type in your problem to find the answer? Unfortunately not. Most calculators are only programmed to deal with common logarithms (logs with base 10) and natural logarithms (logs with base e - 2.718. . . ). If you have a problem with base 4 or base 7, your calculator probably is not programmed to figure out the logarithm.
Fortunately, there is a formula you can use to change your logarithm so that it has a base your calculator can handle. This is called the Change of Base Formula.
Fortunately, there is a formula you can use to change your logarithm so that it has a base your calculator can handle. This is called the Change of Base Formula.
You can use this formula to rewrite a logarithm into the quotient of two logarithms with any base c that you choose. Most of the time, you'll use this formula to change your log into something that you can plug into your calculator so you'll want to choose the new base to be either 10 or e. It doesn't matter. Here's what the formula simplifies to if you use a common log or a natural log (remember ln is a lowercase L for log and n for natural).
You can use either one, you'll get the same answer either way. Let's try an example. We'll start with a logarithm with base 7. Most calculators don't have a log button with base 7 so you'll have to use the change of base formula to rewrite it first.
Example 1
This means 7 to what power will equal 938? 7 to the 3rd power is 343 and 7 to the 4th power is 2401. This tells us that the exponent must be some decimal in between 3 and 4. Since our calculator doesn't have a log base 7 button, we need to use the change of base formula to get the answer. Our calculator does have a common log button (log) and a natural log button (ln) so we can change it to either one. Let's use the common log for this example. This means we'll use the simplified formula:
This means we can rewrite our log as the log (base 10) of 938 divided by the log (base 10) of 7.
Our calculator can't figure out a log of base 7, but it's programmed to figure out common logs! Now we can just type in log938 and log7 into the calculator and divide to get the answer.
Example 2
This problem wants us to figure out what the exponent should be so that 4 to some power equals 15. We know that 4 to the 2nd power is equal to 16. This tells us that the logarithm will be a decimal just under 2. Our calculator isn't programmed to handle logs with base 4, so we need to use the change of base formula to find the answer. You can use the change of base formula to change the base to whatever you want. This time, we'll change it to natural logs with base e - most calculators have an ln button (that's a lowercase L for log, n for natural).
We'll use this simplified version of the change of base formula, this time to switch it to natural logs:
This means we can rewrite our logarithm as the natural log of 15 divided by the natural log of 4.
Now we can use our calculator to find the values of ln15 and ln4, then divide those values to find the answer. Sure enough, the answer is a decimal just under 2.
Change of Base Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.
|
Powered by Interact |