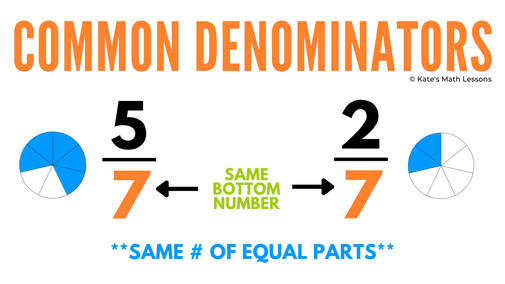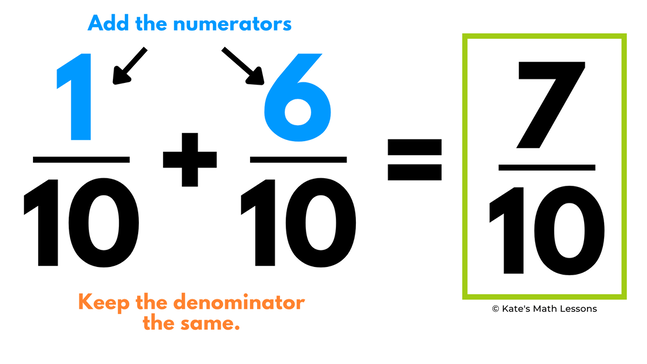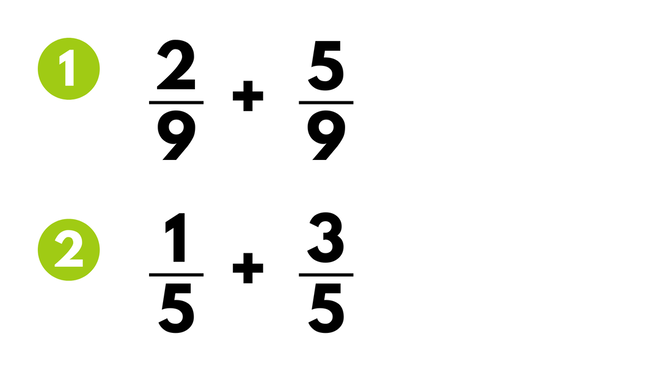Accompanying Resources: Adding Fractions Boom Cards,  Digital Fraction Activities, Printable Study Guide,

​What is a Common Denominator?

First, let's make sure we understand the different parts of a fraction: the numerator and denominator.  The numerator is the first number on the top of the fraction and the denominator is the second number on the bottom of the fraction.

The denominator of a fraction is the number of equal parts that the whole has been split into.  For example, if the fraction is 1/6, that means the whole has been split into 6 equal parts and you have 1 of the 6 pieces.  If the fraction is 3/4, that means the whole has been split into 4 equal parts and you have 3 of those pieces.

When we say that fractions have a common denominator, it means they have the same number on the bottom.  When two fractions have a common denominator, that means both wholes have been divided into the same number of equal pieces.

The fractions 5/7 and 2/7 have a common denominator because they both have a 7 in the denominator.  This also tells us that for both fractions, the whole has been split up into 7 equal parts.

It's important to notice that when two fractions have a common denominator, the equal parts will be the same size.  The larger the denominator is, the smaller each piece will be.  The smaller the denominator, the larger each piece is.  When the denominators are the same, the pieces are the same size.

What are Like Denominators?

Common denominators are also sometimes called "like denominators."   So if you're told that two fractions have like denominators, that just means they have the same bottom number.  

How Do You Add Fractions?

In order to add fractions, the fractions must have a common denominator.  We need the pieces of each fraction to be the same size to combine them together.

Let's say we need to add 2/7 and 3/7 together.  These two fractions have the same denominator, so the equal parts that the whole has been split into are the same size.  Since the pieces are all the same size, we can add these two fractions together.

Welcome to Kate's Math Lessons!  
Teachers,make sure to check out the study guides and activities.

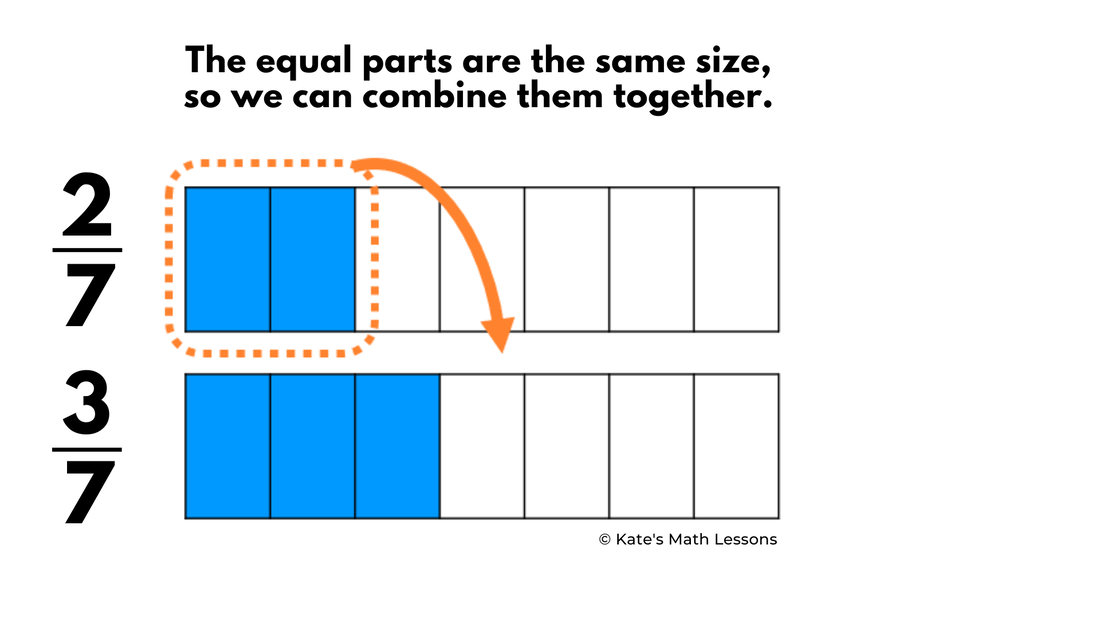
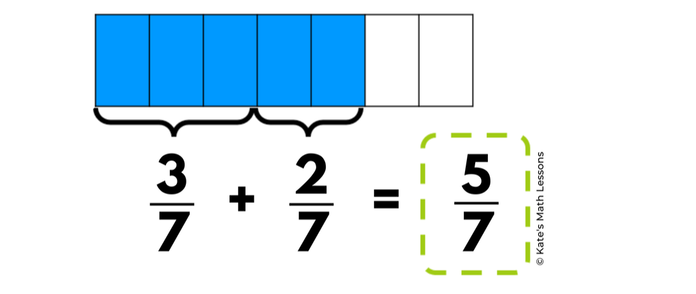
We can add 2/7 to the 3/7 by filling in an additional 2 boxes in the diagram.  We can see that this gives us a sum of 5/7.  (2 parts plus 3 more parts equals 5 parts out of 7 total)

If you're adding two fractions with a common denominator, you can combine them together by adding the numerators together (the top numbers).  The denominator will always stay the same because the size of the equal pieces does not change when you combine the two fractions together.

For example, let's say you have 1/10 + 6/10.  They have the same denominator, so they can be combined together.  Add the numerators (1 + 6 = 7).  Keep the denominator the same (the bottom number stays a 10). 

Remember, the denominator does not change because the sizes of the pieces stay the same.  You're just counting up the total number of pieces when you add the two fractions.
​
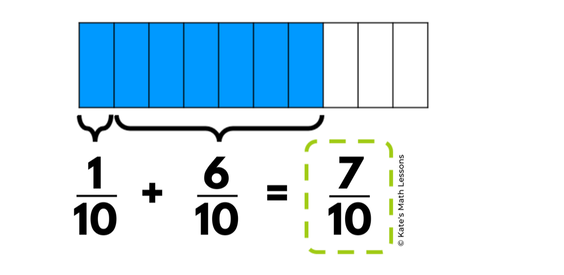
Here's a visual way to look at the same problem:

Adding Fractions Examples

Try adding these fractions on your own and then scroll down to see if you're correct!  When in doubt, it can help to draw a picture to help you visualize the problem.

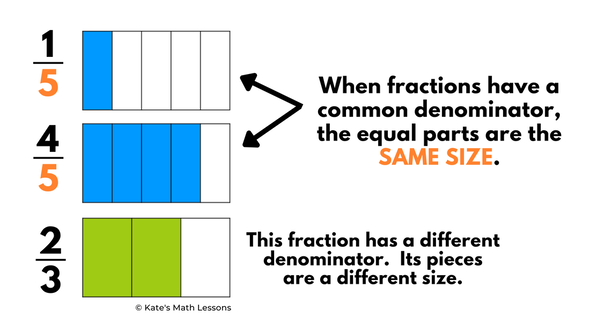
Before you add the fractions, make sure to check that they have the same denominator!  If the denominators are different, we can't combine them because the pieces are not the same size.  

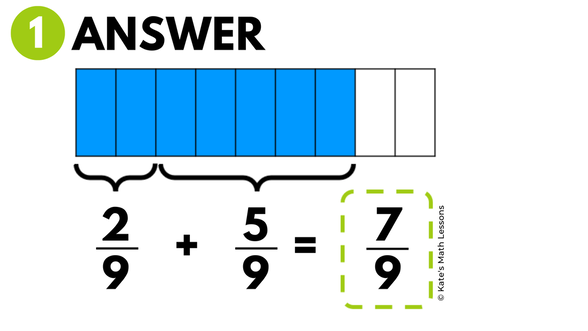
In the first problem, both the denominators are 9 so they have a common denominator.  We can add the fractions 2/9 and 5/9 together by adding the numerators and keeping the same denominator.  This gives us the fraction 7/9.

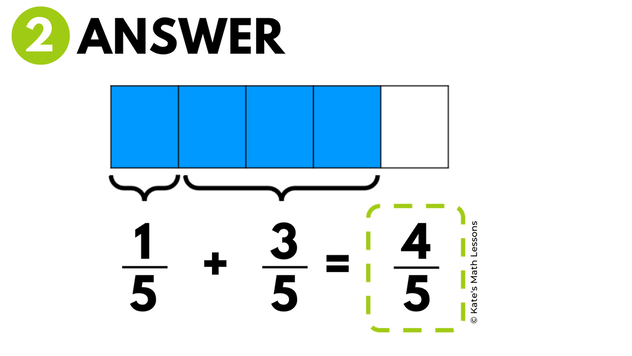
In the second problem, both fractions have a common denominator of 5.  This means we can add the numerators together (the 1 and the 3) and keep the same denominator (there are a total of 5 pieces in the whole).  This gives us the sum of 4/5.

Adding Fractions Common Mistake

A common mistake I see students make when they are adding fractions is that they accidentally add both the numerators and denominators.   Don't add the bottom numbers!  The denominator tells you how many equal parts there are in the whole, this number will stay the same when you add fractions.

​Video

Want to see some more examples? Check out the short adding fractions video below.

Practice Adding Fractions

Think you're ready to try adding fractions on your own? Click the START button below to try a practice quiz.

Powered by Interact

​Ready to learn how to add or subtract fractions with different denominators?
Want to learn how to multiply fractions or divide with fractions?