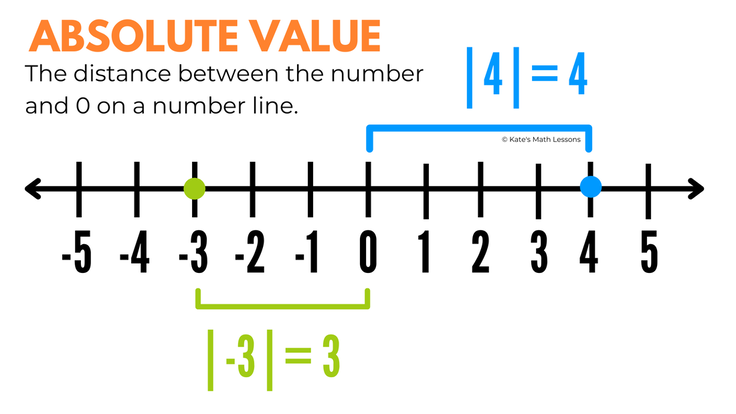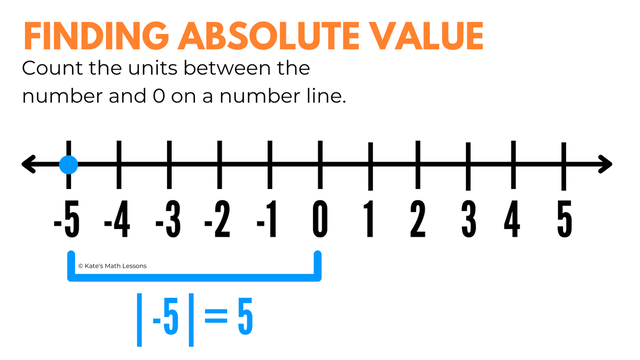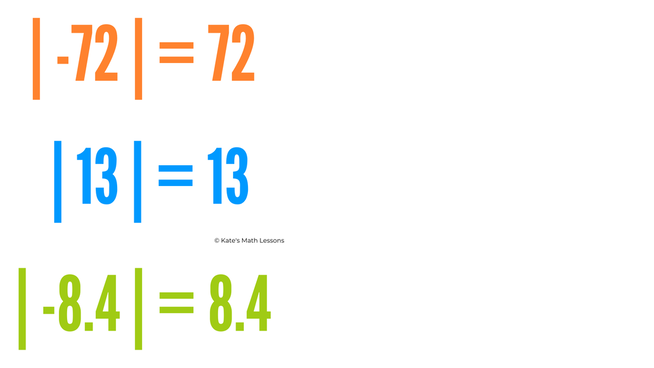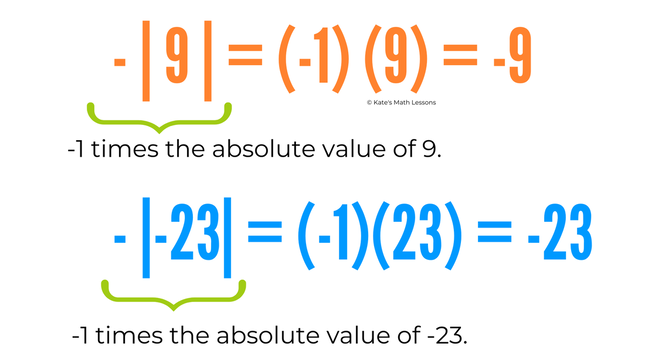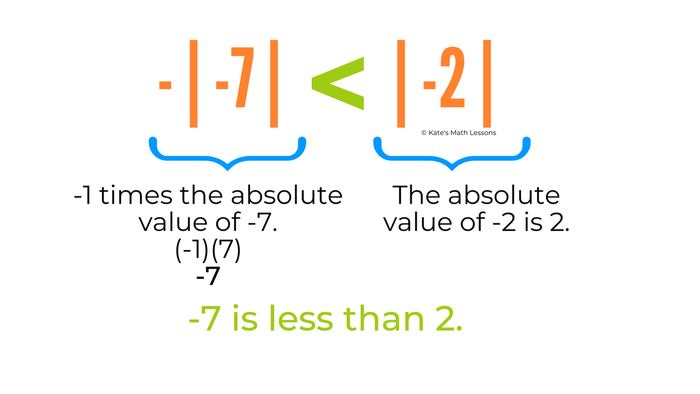Absolute Value and Opposites Activities
What are Absolute Values?
Looking for the definition of absolute value? The absolute value of a number is its distance from zero on a number line. For example, the absolute value of 4, written as |4|, is 4 because it is 4 units away from 0 on a number line. The absolute value of -3, written as |-3| is 3 because it is 3 units away from 0 on a number line.
Remember, distance is never negative. Would you ever tell someone you live -2 miles away? Of course not! When we measure distance, it's always positive or 0. This means the absolute value of a number will never be negative.
How to Find Absolute Value
You can always use a number line to calculate absolute value. You simply count the units between the number and 0. To find the absolute value of 5, written as |5|, you can plot the number 5 on a number line and count the units between -5 and 0. You can see it's 5 units away so the absolute value of -5 is just 5.
The more you do this, you'll hopefully start to see a pattern. Do you see the shortcut to finding absolute value? Can you find the absolute value of -62 without drawing a number line?
The shortcut to finding the absolute value of a negative number is just to drop the minus sign! Remember, distance is never negative. If you have a negative number, just make it positive and that will be its absolute value. If you start with a positive number, just leave it the same.
The shortcut to finding the absolute value of a negative number is just to drop the minus sign! Remember, distance is never negative. If you have a negative number, just make it positive and that will be its absolute value. If you start with a positive number, just leave it the same.
Absolute Value Examples
Here are a few more examples to help you understand absolute values.
Absolute Value Calculator
When I type in absolute value into Google, I can see that students are trying to look up things like "absolute value calculator." Do you really need this? It will take you much longer to use an absolute value calculator for each question on your homework assignment than to just figure it out for yourself!
Remember, absolute value is just the distance from 0 on a number line. Imagine a number line and think about how far that number is from 0. Distance is never negative, so make sure you never give a negative answer for the absolute value of a number.
Remember, absolute value is just the distance from 0 on a number line. Imagine a number line and think about how far that number is from 0. Distance is never negative, so make sure you never give a negative answer for the absolute value of a number.
Absolute Value of 0
Can absolute values be 0? Yep! The absolute value of 0 is 0 because the distance between a number and itself is just zero.
What is the Opposite of a Number?
The opposite of a number is the number that's the same distance from 0 on a number line, but on the other side of the number line. For example, 4 and -4 are opposites. They are both 4 units away from 0 on a number line and are on opposite sides of the number line from 0 (one is to the left of 0 and one is to the right of 0).
Opposite of a Number Examples
To find the opposite of a number, you can just multiply the number by -1. Or just add/remove a minus sign to find the opposite! Here are a few more examples of opposites to help you.
Are Opposites and Absolute Value the Same Thing?
This is another question that I commonly get from students. The answer is no, absolute value and opposites do not mean the same thing.
I can see why it might seem like they're the same. If you start with a negative number, its opposite and absolute value will be the same number. For example, the absolute value of -7 is 7 and the opposite of -7 is also 7. The opposite and absolute value of a negative number are the same.
The problem is when you start with a positive number. The opposite and absolute value of a positive number are NOT the same! For example, the absolute value of 6 is 6. But the opposite of 6 is -6.
I can see why it might seem like they're the same. If you start with a negative number, its opposite and absolute value will be the same number. For example, the absolute value of -7 is 7 and the opposite of -7 is also 7. The opposite and absolute value of a negative number are the same.
The problem is when you start with a positive number. The opposite and absolute value of a positive number are NOT the same! For example, the absolute value of 6 is 6. But the opposite of 6 is -6.
Negative Signs In Front of an Absolute Value
Now that we've looked at absolute values and opposites of numbers, let's talk about problems that are a little trickier: when there's a minus sign in front of the absolute value bars.
Here's an example: -|-4|
This looks much worse than it is. One way to think about this is that it's really the same thing as a -1 being multiplied by the absolute value of -4.
We can rewrite it like this: -|-4| = (-1) |-4|
With this type of problem, you find the absolute value of -4 first, and then multiply that number by -1.
-|-4| = (-1) |-4| = (-1) (4) = -4
Another way to think about this kind of problem is that the negative sign out front is telling you to find the opposite of the absolute value of -4.
-|-4| = opposite of |-4| = opposite of 4 = -4
Here are a few more examples with negative signs in front of absolute value bars:
Here's an example: -|-4|
This looks much worse than it is. One way to think about this is that it's really the same thing as a -1 being multiplied by the absolute value of -4.
We can rewrite it like this: -|-4| = (-1) |-4|
With this type of problem, you find the absolute value of -4 first, and then multiply that number by -1.
-|-4| = (-1) |-4| = (-1) (4) = -4
Another way to think about this kind of problem is that the negative sign out front is telling you to find the opposite of the absolute value of -4.
-|-4| = opposite of |-4| = opposite of 4 = -4
Here are a few more examples with negative signs in front of absolute value bars:
Comparing Absolute Values
Sometimes you'll be asked to compare two values and absolute value signs might be involved. You might be asked which value is larger or smaller, or you might be asked to write an inequality to compare the two numbers. Let's look at an example.
1) Which is larger? |-5| or 3?
With these types of problems, you'll want to simplify expressions with absolute value signs first and then compare the two numbers. In this example |-5| = 5 so you're really comparing 5 and 3. Which one is larger? 5. So you could circle the |-5| as your answer.
If you needed to write an inequality to compare them, you could use the greater than sign > and write |-5| > 3.
Let's look at a second example.
2) Write an inequality to compare -|-7| and |2|.
Before we compare them, let's simplify each expression first. -|-7| is the same thing as -1 times the absolute value of -7. This simplifies to -7. The absolute value of 2 is just 2 so we're really comparing the numbers -7 and 2.
-7 is smaller than 2 so we can use the less than sign < to write -|-7| < |2|.
1) Which is larger? |-5| or 3?
With these types of problems, you'll want to simplify expressions with absolute value signs first and then compare the two numbers. In this example |-5| = 5 so you're really comparing 5 and 3. Which one is larger? 5. So you could circle the |-5| as your answer.
If you needed to write an inequality to compare them, you could use the greater than sign > and write |-5| > 3.
Let's look at a second example.
2) Write an inequality to compare -|-7| and |2|.
Before we compare them, let's simplify each expression first. -|-7| is the same thing as -1 times the absolute value of -7. This simplifies to -7. The absolute value of 2 is just 2 so we're really comparing the numbers -7 and 2.
-7 is smaller than 2 so we can use the less than sign < to write -|-7| < |2|.
Absolute Values Game
There's a fun game you can play to help you practice finding absolute values! It's very similar to the game War, but with black cards representing positive numbers and red cards representing negative numbers. Take out all the face cards and jokers and divide the deck between two people.
1) Each player lays down one card at a time.
2) Find the absolute value of each card. The player with the highest absolute value wins that round and takes both cards.
3) Continue until all cards have been played. The player with the most cards wins!
It can be fun to play with these oversized decks of cards (affiliate link) or use this digital random card generator to play virtually.
Here's an image you can pin to save this absolute value and opposites lesson for later:
1) Each player lays down one card at a time.
2) Find the absolute value of each card. The player with the highest absolute value wins that round and takes both cards.
3) Continue until all cards have been played. The player with the most cards wins!
It can be fun to play with these oversized decks of cards (affiliate link) or use this digital random card generator to play virtually.
Here's an image you can pin to save this absolute value and opposites lesson for later: