|
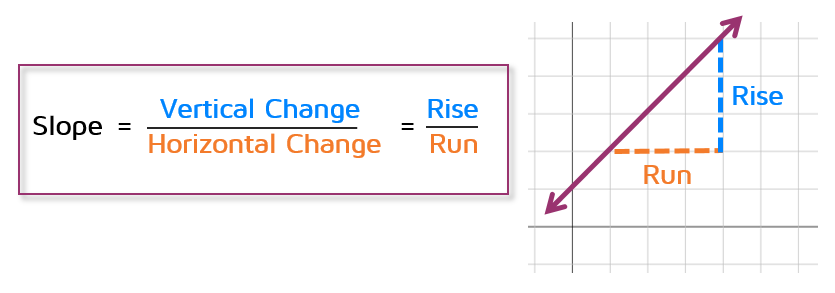
Using Two Points to Find Slope Page 1 of 5 Accompanying Resources: Slope Google Activity, Printable Study Guide, FREE Activity, Task Cards, Boom Cards (digital task cards) What is Slope?Slope measures the steepness of a line. It's measured as the ratio of the amount of horizontal change to the amount of vertical change, or "Rise over Run." You can use a graph to find slope by counting spaces to find the rise and run.
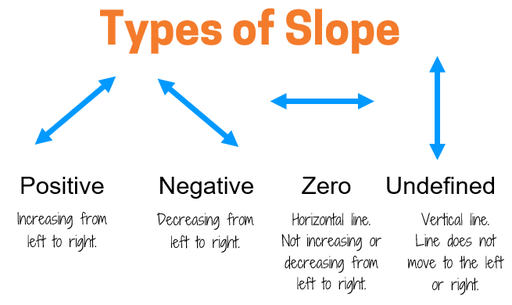
There are 4 different types of slope based on the direction of the line. Check out the intro to slope lesson to learn more about each type. You can use a graph to find the slope of a line, but it's possible to find the slope without one. If you're given two points that are on the line, there is a formula that you can use to find the slope of the line. You can always pull out graph paper to find the slope, but you may find that the formula for slope can be faster and easier. |
|