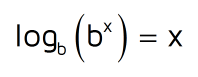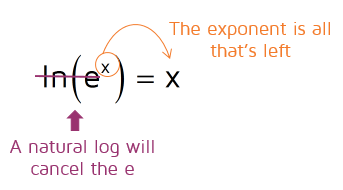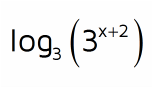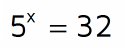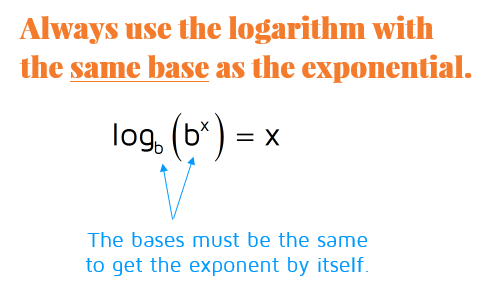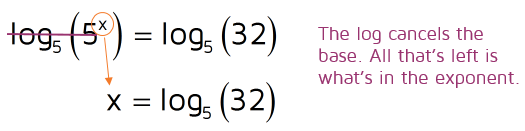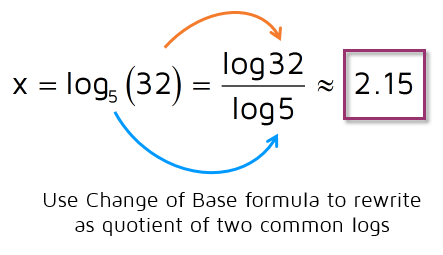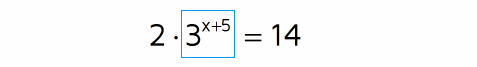What's an Exponential Equation?An exponential equation is an equation with a variable in the exponent. Here's a few examples of exponential equations:
Sometimes it helps to see a non-example to make sure you understand a definition. Don't confuse an exponential equation with an equation like this:
|
|
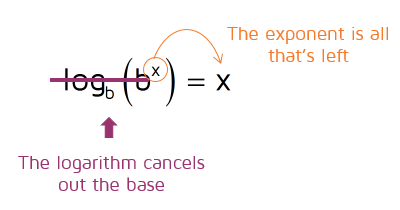
What does this mean? If the logarithm and exponential expression have the same base, they cancel each other out! All that's left is what's in the exponent.
Here's a more visual way to look at this property:
As long as you're using a logarithm that has the same base as the exponential expression, it will cancel out the base. The only thing that will be left is what was in the exponent.
There's a special case of this property that applies to natural logs (ln). A natural log has a base of e (e is a constant approximately equal to 2.71828. It's kind of like pi, it's just a number that's used so often it gets its own special symbol). If the base of the exponential is e, you'll want to use the natural log to cancel out the e. (Not sure what a natural log is? Learn more in the intro to logarithms lesson.)
Let's look at a few quick examples that use these properties before we start actually solving equations.
Simplify the expression below.
Remember, the property only works when the logarithm and the exponential equation have the same base. In this problem, the logarithm has base 3 (the little number after the word log) and the exponential expression in the parentheses also has a base of 3. Since they have the same base, they cancel each other out! All that's left is what's in the exponent: the x + 2.
Here's one more example of this property.
Simplify the expression below.
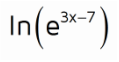
A natural log (ln) is just a logarithm with a base of e. Since ln has a base of e and the exponential expression also has a base of e, they cancel each other out. The only thing that's left over is what was in the exponent: the 3x - 7.
Solving Exponential Equations
Now that we can see how a logarithm can cancel the base, we'll use this property to help solve exponential equations. Remember, an exponential equation has the variable in the exponent. If we can use a logarithm to cancel out the base, all that's left is what's in the exponent. This will leave us with a much simpler equation to solve.
Example 1
Solve for x.
Example 1
Solve for x.
This is an exponential equation because the x is in the exponent. In order to solve for x, we need to get rid of the 5. The 5 is the base of the exponential expression. To cancel it, we need to use a logarithm with the same base.
Step 1: Take the log of both sides.
Remember, when you're solving equations you always need to do the same thing to BOTH sides. So if we take the logarithm of the left side to cancel the 5, we also need to take the logarithm of the right side too.
Why did we use a logarithm with base 5? In order to get the exponent by itself, we need to cancel out the 5 that's the base of the exponential. If we use the logarithm with the same base, they'll cancel out and we'll be left with only what's in the exponent.
We took the logarithm of base 5 of both sides in order to cancel out the base 5 in the exponential. This means the only thing that's left is the x.
We have x all by itself now on the left-hand side. That's great! Now all that's left to do is figure out what the right-hand side is. There aren't any variables on the right, it's just a logarithm that needs to be evaluated. Your calculator probably doesn't have a log base 5 button on it, so we need to use the Change of Base formula to evaluate it.
Here's the Change of Base formula in case you need a refresher:
We can use this formula to evaluate the logarithm on the right side of the equation. We'll use the Change of Base formula to rewrite it using common logs. Then we can use the log button on the calculator to find the answer.
Step 2: Use the Change of Base formula to rewrite the log.
Your calculator should have a log button on it. You just plug in log32 and divide by log5 to get approximately 2.15 as the answer for x.
Step 3: Check your answer.
How do we know that this answer is right? We can check it by plugging 2.15 into the original equation.
If you actually plugged 5 to the 2.15 in on your calculator, you may have noticed that it actually comes out to about 31.83 or so. Why doesn't it come out exactly to 32? Because 2.15 is a rounded answer. Anytime you round to get your answer, it will be a little bit off when you go to check your answer.
Example 2
Solve for x.
Solve for x.
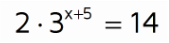
It's important to always get the exponential term by itself before you use a logarithm to cancel the base.
Step 1: Isolate the exponential term first.
Get the exponential term by itself before you use a logarithm. We need to undo the multiplication by 2 first before we can try to get x out of the exponent.
Step 2: Take the log of both sides.
Now that the exponential term is by itself, we need to use a logarithm to cancel the base 3. We need to use a logarithm with the same base to do this. The exponential term has a base of 3 so we need to use a logarithm with a base of 3 on both sides. Make sure to always do the same thing on BOTH sides of the equation to keep things balanced.
Step 3: Use the Change of Base formula to rewrite the log.
We're almost done! Remember, the log base 3 of 7 on the right side is just a decimal. If you need an exact answer, you could leave the expression on the right as it is. Most of the time, your teacher will ask you for a rounded answer so let's use the Change of Base formula next to approximate the log base 3 of 7.
Step 4: Solve for x.
Now all that's left to do is to get rid of the 5 and we'll have x by itself.
Step 5: Check your answer.
It's always a good idea to check your answer if you can. Remember, -3.23 is a rounded answer so it won't work out exactly right when we check it, but should be very close. Always go back to the original equation when you check your answer.
Exponential Equations Video
Practice
Ready to try some problems on your own? Click the START button below to try a practice quiz.
|
Powered by Interact |