Substitution Method            Page 1 of 5
​Accompanying Resources: Activity for Google,  Study Guide, Fun Activity, Boom Cards, Assessment

​What's a System?

A system of equations is a set of 2 or more equations. The systems you study in Algebra 1 generally consist of two linear equations.  The graphs of linear equations are straight lines, so the goal is to figure out the point where the two lines cross.  This ordered pair will be the solution to the system. The solution to a system is the point that works for all of the equations in the system.  ​

​When your system has two linear equations, there are 3 things that can happen.
1) The lines will cross at one point. This means there will be one solution to the system.
2) The lines will be parallel and never cross. This means there is no solution.
3) The lines will be the same and lay right on top of each other. If this happens, there will be infinitely many solutions because each point on the line works for both equations.

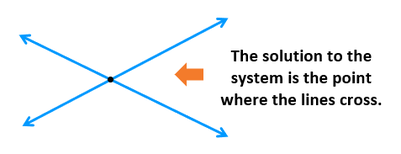
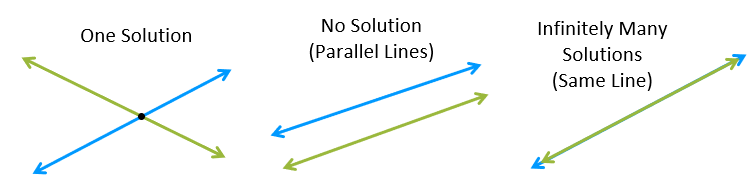
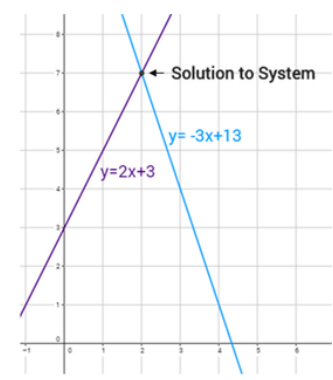
In this lesson, we'll focus on systems that have one solution. The system shown to the right consists of two linear equations: y = 2x + 3 and y = -3x + 13.

You can see from the graph that the two lines cross at the point (2,7). This means that the solution to this system is (2,7).  If you plug in 2 for x and 7 for y, they work in both​ equations.

​You can always graph the equations in a system to find the solution point. However, it can be difficult to tell where the lines cross if the answer is very large or if the answer involves fractions. The substitution method is an alternative to graphing. It's a method that can be used to solve a system without graph paper and you'll get an exact answer every time.

Welcome to Kate's Math Lessons!  

Teachers,make sure to check out the study guides and activities.

1      2      3      4      5