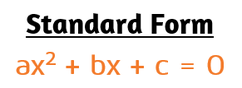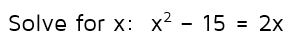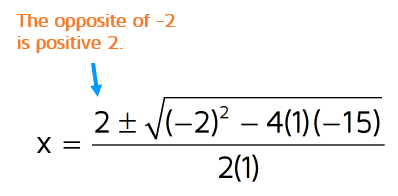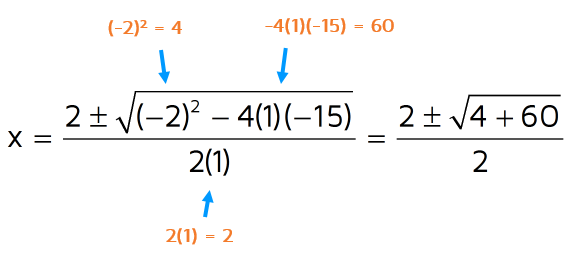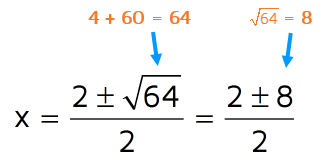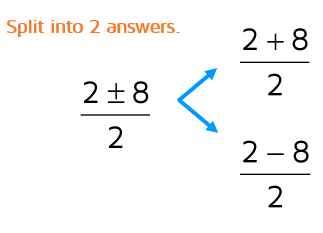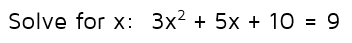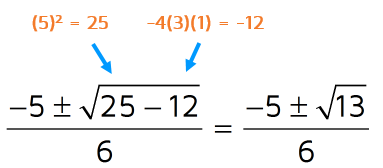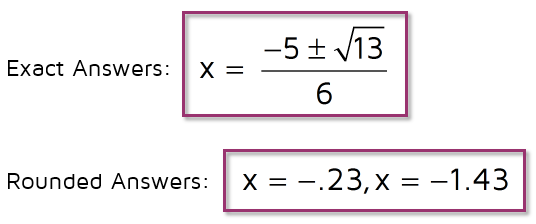​Accompanying Resources: Printable Study Guide, Google Drive Activity, Printable Fun Activity, Boom Cards (digital task cards)

​Standard Form of a Quadratic Equation

A quadratic is a polynomial whose highest exponent is 2.  The standard form of a quadratic equation is written below.  

When a quadratic equation​ is written in standard form, the x-squared term will be written first. The x-term will be next and the constant will be last.  The equation must be set equal to 0 for it to be in standard form.

There are several different methods you can use to solve a quadratic equation.  The Quadratic Formula is one method you can use.  In order to use the Quadratic Formula, the equation must be in standard form.
If it's not in standard form, you'll have to do some rearranging to get everything in the right order.  After you get your equation in standard form, you'll need to identify the values of a, b, and c.  a will always be the coefficient of the x-squared term, b will be the coefficient of the x-term, and c will be the constant at the end.
​
Look at the examples in the table below to see how to rewrite a quadratic in standard form and identify a, b, and c.

Solving Quadratic Equations

​It's pretty straightforward to solve a linear equation like 2x + 5 = 11.  You subtract 5 from both sides and divide by 2.  Done. Unfortunately, quadratic equations are a little more complicated to solve. There are a few different methods you can use to solve them. You can solve a quadratic equation by graphing, factoring, or completing the square. You can also the Quadratic Formula to solve a quadratic equation.

Welcome to Kate's Math Lessons!  

Teachers,make sure to check out the study guides and activities.

What is the Quadratic Formula?

The Quadratic Formula is a formula you can use to find the solutions of a quadratic equation that's written in standard notation.  In the formula, the a is the coefficient of the x-squared term.  The b is the coefficient of the x-term.  The c in the formula is the constant.  One way to read this formula aloud is to say "x equals the opposite of b, plus or minus the square root of b-squared minus 4ac, divided by 2a."

Pay attention to the -b in the numerator of the formula.  This is the opposite of b.  -b is the same as -1b.  When you multiply a number by -1, it changes the sign.  Always make sure to switch the sign of the b value when you plug it in the formula.  

Also pay attention to the b-squared term under the square root.  If b is negative, b-squared will be positive because a negative times a negative equals a positive.

How Do You Use the Quadratic Formula?

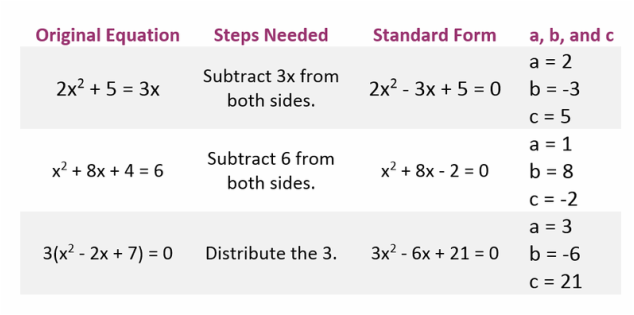
Step 1: Make sure the quadratic equation is in Standard Form. Rearrange if necessary.
Step 2: Identify a, b, and c.  Pay close attention to plus and minus signs.
Step 3: Plug a, b, and c into the formula.  
Step 4: Simplify.
           a) First simplify the numerator and denominator.
           b) Split into two answers. One with a + sign, one with a - sign.
           c) Simplify the two numerators if possible.
           d) Divide last.

Example 1

Step 1:  We need to rewrite this equation in standard form before we can use the Quadratic Formula.  We can subtract 2x from both sides to get it set equal to 0.

Step 2: Now that it's in standard form, we can identify the values of a, b, and c.  a is the coefficient of the x-squared term.  When there isn't a number written in front of a variable, the coefficient is 1 so a = 1.  b is the coefficient of the x-term.  There's a minus 2x, so b = -2.  c is the constant at the end (the number without a variable) so c = -15.

a = 1, b = -2, c = -15

Step 3: Now plug in the values for a, b, and c.  Make sure to switch the sign of b when you use the formula!

Step 4: Simplify.  The denominator is easy: 2(1) = 2.  In the numerator, start with the part under the square root.  -2 squared is a positive 4 (a negative times a negative is positive).  

Now we can simplify what's under the square root.  4 + 60 = 64 and the square root of 64 is 8.

Next, we need to split this up into two separate answers.  The symbol between the 2 and the 8 is a plus or minus symbol.  This means we need to split it up and write one answer with a + sign and the other with a - sign.

 
After you've split it up into two separate answers, see if you can do any more simplifying.  2 + 8 = 10 and 2 - 8 = -6, so we can simplify both numerators.  Save the division until the very end when you have it down to just one number in the numerator.  10 divided by 2 is 5 and -6 divided by 2 is -3.  

​Example 2

​Step 1:  We need to rewrite this equation in standard form before we can use the Quadratic Formula.  We can subtract 9 from both sides to get it set equal to 0.

Step 2: Identify a, b, and c.  a = 3, b = 5, c = 1

Step 3: Plug the values into the formula.  Don't forget to switch the sign of b.

 
Step 4:  Simplify.  The denominator is easy: 2(3) = 6.  In the numerator, simplify the part under the square root first.  5 squared is 25.  -4(3)(1) is -12.  25 -12 = 13, so you're left with a 13 under the square root.

In the first example, we ended up with a 64 under the square root and we were able to simplify it to 8.  In this case, we can't simplify the square root of 13 (Check out the lesson on simplifying radicals if you need a refresher). This means we can leave the answer just like this if we want an exact answer.  If you want a rounded answer, you can plug the square root of 13 into your calculator (it's about 3.61) and use that to get two rounded answers.

Quadratic Formula Video

Practice

Ready to try using the quadratic formula on your own? Click the START button below to take a practice quiz.

Powered by

​Want to see a different way to solve a quadratic equation?
Check out the completing the square lesson or the solving a quadratic by factoring lesson.