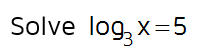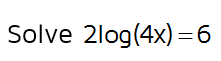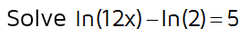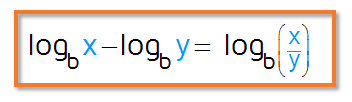​Accompanying Resources: Printable Study Guide, Google Drive Activity

​Logarithms Review

New to logarithms? Make sure to check out the intro to logarithms lesson first.  Before we look at solving equations with logarithms, let's do a quick review of logarithms in general.  A logarithm answers a question like this: 2 to what power will equal 128?  

You can always rewrite a logarithmic equation as an exponential equation.  They're both going to have the same base.  The small number written after the word log is the base of the logarithm. The logarithm above has a base of 2.  The logarithm is always equal to the exponent.  

When you rewrite a logarithm in exponential form, remember that both forms use the same base.

Solving Equations with
​Logs on One Side

To solve a logarithmic equation with a logarithm on one side, you first need to get the logarithm by itself (we'll do an example so you see what we mean).  Next, identify the base of the logarithm in the equation and use the same base to rewrite it in exponential form.  Once you rewrite the equation in exponential form, it should simplify to an easier equation that you can solve.

Example 1

Welcome to Kate's Math Lessons!
​Teachers - don't miss the study guides and activities! 

This equation has a logarithm already by itself on one side, so we can start by rewriting it in exponential form.  To do this, we need to identify the base of the log, since we need to use the same base when we change it to exponential form.  The small number written after the log is the base - so the base of this logarithm is 3.  Now we need to rewrite it in exponential form using 3 as the base.  

Now that we have it in exponential form, we can simplify the left side.  3 to the 5th power is 243.  This means that x = 243.

Example 2

Before we can rewrite this equation in exponential form, we need to get the logarithm by itself. We can do this by dividing both sides by 2.

Now that the log is by itself, we can rewrite it in exponential form.  To do this, we need to identify the base.  There isn't a small number written after the base - that means you can assume it's a common log with base 10.  We need to use 10 as the base when we rewrite it in exponential form.

Now that the equation is in exponential form, we can simplify the left side and then solve for x.  10 to the third power is 1000.  This gives us 1000 = 4x.  We can solve for x by dividing both sides by 4.  This means that x = 250.

Example 3

This equation is a little bit harder because it has two logarithms. Before we can rewrite it as an exponential equation, we need to combine the two logs into one.  We can do this using the difference of two logs rule. (Doesn't sound familiar? You might want to check out the lesson on logarithm rules before moving on.)  

Here's the difference rule for logarithms:

Since we have two logarithms with the same base (they are both natural logs with base e), we can use the rule above to combine them into one logarithm.

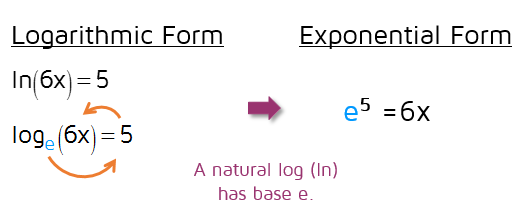
Now that we've rewritten the equation so it has a logarithm by itself, we can rewrite it in exponential form.  Whenever you rewrite a logarithm, make sure to identify the base.  We have a natural log (remember, ln is a lowercase L for log and an n for natural).  This means the base is the irrational number e (e is approximately equal to 2.71828).  You can learn more about natural logs in the intro to logarithms lesson.

After the equation has been written in exponential form, it's relatively easy to solve for x.  If you want to leave it as an exact answer, just divide both sides by 6 and leave e in your answer.  If you want an approximate answer, you can do e to the 5th power on your calculator and then divide by 6.  If your calculator doesn't have an e button, you can use 2.71828 to approximate e.

​Video

Want to see another example? Check out the short video below.

Practice

Ready to try solving some equations on your own? Click the START button below to try a practice quiz.

Powered by Interact

Want to learn how to solve a different type of logarithmic equation?
Check out the lesson on solving logarithmic equations with logs on both sides.