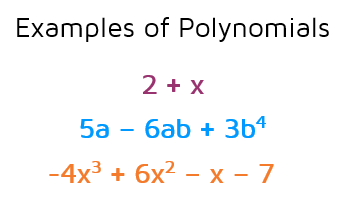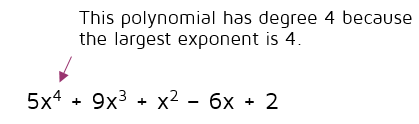|
|
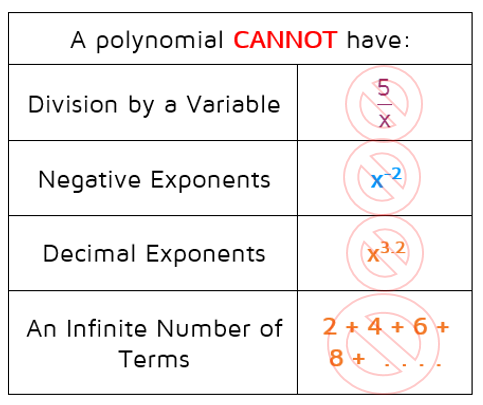
A polynomial can never have a variable in the denominator of a fraction (no division by a variable). A polynomial can have fractions, as long as there are only numbers and no variables in the denominator.
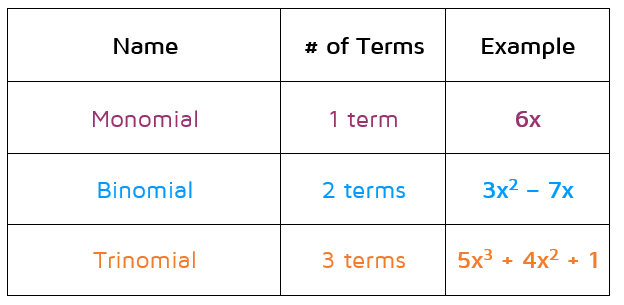
Names of Polynomials
There are a few names given to polynomials based on the number of terms. Technically the prefix poly means "many," but the word polynomial includes expressions with only one term as well. Monomials, binomials, and trinomials are just specific types of polynomials. A polynomial can have more than 3 terms, they just don't get a special name and are just referred to as polynomials.
If you're familiar with prefixes, you can remember these names if you know that the prefix mono means "one," the prefix bi means "two," and the prefix tri means "three."
Degrees of Polynomials
Polynomials are often classified based on their degree. If there is only one variable involved, the degree of the polynomial is the largest exponent of that variable.
If there are several variables in the polynomial, you need to look at each term individually and add the exponents of the variables together to find the degree of each term. The highest degree you find is the degree of the whole polynomial.
Want to learn more about polynomials? Check out the lesson on adding and subtracting polynomials.