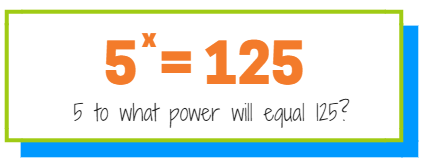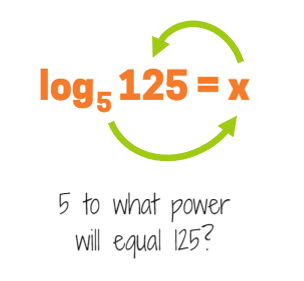Intro to Logarithms            Page 1 of 3
Accompanying Resources: Study Guide, Task Cards/Boom Cards, Google Drive Activity

​Review of Inverses

Before we talk about logarithms, let's do a quick review of inverses.  Inverse operations are operations that "undo" each other.  For example, addition and subtraction are inverses. If you add 5, you can easily undo that by subtracting 5.  Multiplication and division are also inverses. If you multiply a number by 3, you can undo that by dividing by 3.

Logarithms

​So what's a logarithm? It's an operation that will undo an exponent.  Logarithms are the inverses of exponential functions.  Why the funny name? You'll have to ask John Napier - he came up with the name back in the 1600s.  We use logarithms to go backwards and solve an exponential equation. They help us figure out this type of problem:

We can use a logarithm to figure out what the exponent must be for this to come out to 125.  In the exponent above, the base is 5.  That means 5 times itself how many times will equal 125?  A logarithm will tell us the answer.  When we write logarithms, we use the same base that was used in the exponential equation.  The base in this example is 5, so we'll have a logarithm with a base of 5.  

When you write a logarithm, you abbreviate it as "log" and write the base as a small subscript after the word log.

You would read this as "log base 5 of 125 equals x".  It means 5 to what power will equal 125? 

Welcome to Kate's Math Lessons!  

Teachers, make sure to check out the study guides and activities.

Do you know the answer? 5 times itself how many times will equal 125? We know the answer isn't 2 because 5 to the second power is equal to 25.  

​5 to the 3rd power is 5x5x5 = 125.  This means the answer is 3.

 1      2      3