Page 1 of 4
Accompanying Resources:  Task Cards & Boom Cards, Fun Activity, FREE Study Guide

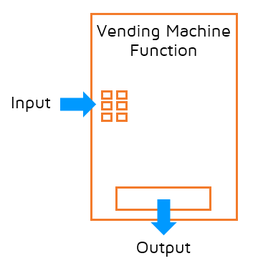
What are Functions?

If you checked out the intro to functions lesson or the lesson on representing functions, you know that a function takes an input value and assigns it exactly one output value. 

Think about a function as a vending machine.  You give the function an input value (the code you type in) and it assigns you an output (candy, pretzels, etc.).  If you enter the same input code the next time, it should give you the exact same output that it gave you the last time.

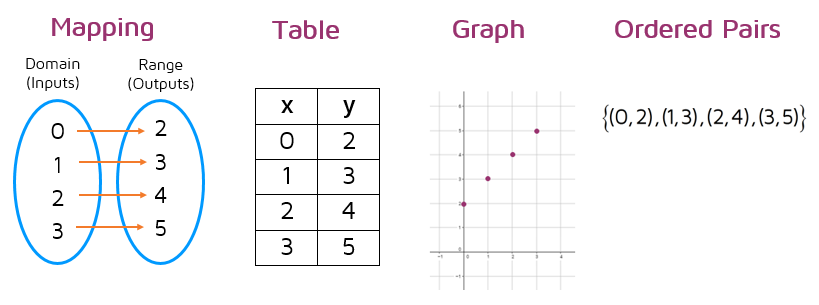
Representing Functions

There are several different ways to represent a function.  Mapping diagrams use ovals and arrows to show how the inputs and outputs are matched up.  You can also use tables, graphs, or a set of ordered pairs to represent a function.

1      2      3     4

Welcome to Kate's Math Lessons!  

Teachers: make sure to check out the study guides and activities.