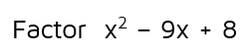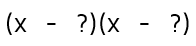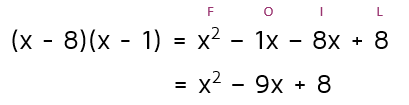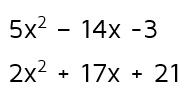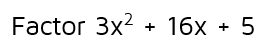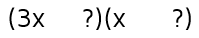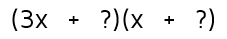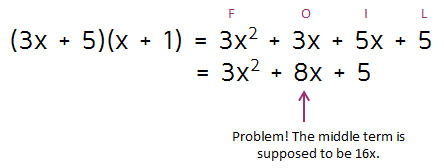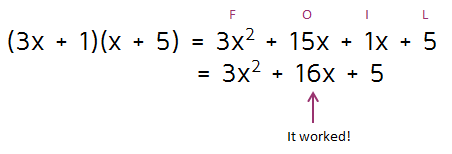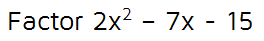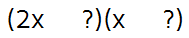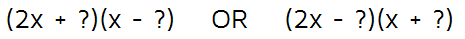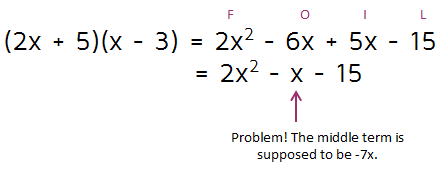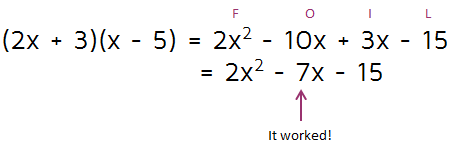Factoring Quadratics

This lesson addresses some more difficult factoring problems. If you would like to see some easier problems before you try these, check out the Level 1 Factoring lesson (quadratic expressions with a leading coefficient of 1). This lesson shows you how to factor an expression with a number in front of the x-squared term.

Accompanying Resources: Factoring Task Cards (printable & digital), Number Tile Activities

Factoring Quadratics Task Cards and Boom Cards

Factoring Quadratics Number Tile Activities

Factoring Quadratics Review

In the Level 1 lesson, all of the quadratics we factored started with an x-squared term. Let's look at one quick problem to review before we try some harder ones.

In order to factor this, we need to identify the two binomials that multiply to this quadratic. In other words, we need to know ( ? ) times ( ? ) will equal this quadratic expression. We know that the x-squared term will come from multiplying the "Firsts" if you use FOIL - this means that there must be an x in both Firsts spots. This gives us:

Now let's look at the constant at the end. There's a positive 8 at the end. This means the numbers in the "Lasts" spots must multiply to 8. A common assumption students make is to think that since the two numbers multiply to a positive 8, that they must both be positive. However, two negatives also multiply to a positive, so that tells us that we either have two plus signs or two negative signs. It can't be one of each because then they would multiply to a -8 at the end. So now we have it narrowed down to this:

So which one is it? To tell, always look at the term in the middle. Our term in the middle is -9x. The only way for the middle term to end up negative will be to use the option with two negative signs. This means it must be this:

Next we need to look at the options for the "Lasts" spots. We know they must multiply to 8, so let's list out the options.

Options for Lasts spots:
1 and 8
2 and 4

Now we can just pick a combination and try it to see if it works. Distribute (use FOIL) to see if it comes out to the quadratic we've been given. If it doesn't work, try a different option. Let's try the 1 and 8 first.

Welcome to Kate's Math Lessons!

Teachers: make sure to check out the study guides and activities.

$Picture$

Check answer to factoring problems by using FOIL.

Worked on the first try! This means the final factored answer is (x - 8)(x - 1). The good thing about factoring is that you can always check your answer. If you use FOIL and it didn't come out right, go back and try to find your mistake.

Quadratics with Different Leading Coefficients

All of the quadratics we looked at in the Level 1 lesson started with a x-squared term with a 1 as the leading coefficient. Unfortunately, not all quadratics are this way. What about these quadratics? Quadratics that don't have a leading coefficient of 1 are a little more difficult to factor.

Quadratics with a constant in front of x-squared term

The main difference is that instead of just putting an x in the Firsts spots, you'll have to make some changes.
Let's go through an example.

Example 1

We need to start by thinking about what will go in the Firsts spots. We can't just do x and x like we did in the earlier problems because that would give us a regular x-squared in the front. We need to change it so when we multiply the Firsts, we get a 3 in front of the x-squared term. How do fix this? Easy. Just change one of the x's in the front to a 3x. This gives us:

Next, think about the signs. There are all plus signs in the quadratic we were given, so the factored answer will also have all plus signs. Now we have it down to:

Now we just need to figure out what goes in the Lasts spots. Here's the biggest part where this type of problem is different than the ones in Level 1 - before it didn't matter what order we put the numbers in the Lasts spots. Now it does. We still need the numbers in the Lasts spots to multiply to the constant at the end, but this time it's going to make a difference which one we put first.

The only numbers that multiply to 5 are 1 and 5. So now the only question is - do we put the 5 first or the 1 first? How do you tell? You just pick an option and test it out using FOIL. If the first option you choose doesn't work, try the next one. Let's try putting the 5 first and then the 1.

How to check answer to factoring problem with FOIL

So this option didn't work. When you just have x's in the First spots, it doesn't make a difference what order you put the numbers in the Lasts spots. But if the Firsts terms aren't the same, it will make a big difference if you switch the numbers in the Lasts spots. Let's see what we get if we switch the 5 and the 1 around:

How to check your answer when factoring using FOIL

This time it worked! Did you notice how the middle terms changed when you switched the 5 and the 1 around? The final factored answer for this problem is (3x + 1)(x + 5).

Example 2

Factor quadratic expression with number in front of x-squared term

Always start by thinking about what should go in the Firsts spots. In order to get a 2 in front of the x-squared term, we need one of the Firsts spots to be a 2x and the other to be an x. This gives us:

Next, think about your signs The constant at the end is a -15, so the numbers in the Lasts spots must multiply to -15. The only way to get two numbers to multiply to a negative is to have one be positive and one be negative. Right now, we're not sure which order the signs go in, so we'll have one of these two options:

Don't sweat over where to put the plus sign and where to put the minus sign. Remember, can always fix it later. If we use FOIL and end up with a positive 7x in the middle instead of -7x, we can fix it by just switching the plus and minus signs around.

Now we need to think about the numbers in the Lasts spots. We know they need to multiply to a -15 so we could have 1 and 15, or 3 and 5 (with one positive and one negative - just not sure which one yet). Remember, we also need to think about the order they go in. If one option doesn't work, we need to try switching the order before we move on to the next option. The more you practice factoring, the easier it will be for you to start with the options that are most likely to work. Generally, unless the middle term is really large, it's a good idea to start with the factors that are closer together. So let's start with the 3 and the 5. Don't worry about the signs, we can switch them at the end if we need to.

Check answer to factoring problem by using FOIL

So it didn't work to put the 5 first and then the 3. If we switched the signs around, it would just change the middle term to a positive x. We need a -7x, so that's not going to work. Before we just cross out the 3 and the 5 as an option and move on to the 1 and the 15, we have to try switching the 5 and the 3 around.

How to use FOIL to check answer to factoring problem.

It worked this time! So the final factored answer is (2x + 3)(x - 5). If you don't get it to work right away, make sure you keep trying other options. Be systematic about it - write out the possible options and cross them off as you go so you make sure you don't miss any. This type of quadratic may take a little longer to factor, but there are only a limited number of options to try. And the good thing is that you can always check your answer using FOIL so you'll know if your answer is right.