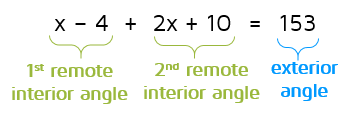|
Accompanying Resources: Exterior Angle Theorem Activity for Google Drive, Angles of Triangles Activity for Google Drive (includes Triangle Sum Thm), Boom Cards (includes Triangle Sum Thm)
|
|
The interior angles of a triangle are the three angles inside the triangle. |
|
Exterior Angles of a Triangle
You may have guessed that exterior angles are on the outside of a triangle, but it's a little more specific than just that. An exterior angle must form a linear pair with an interior angle. This means that the exterior angle must be adjacent to an interior angle (right next to it - they must share a side) and the interior and exterior angles form a straight line (180 degrees).
If you extend one of the sides of the triangle, it will form an exterior angle.
If you extend one of the sides of the triangle, it will form an exterior angle.
There can be multiple exterior angles, it just depends on which sides of the triangle are extended. It can be tempting to think that any outside angle that touches a triangle is an exterior angle. Make sure to remember that an exterior angle must form a linear pair with an interior angle. It needs to share a side with an interior angle and the two together must form a straight line.
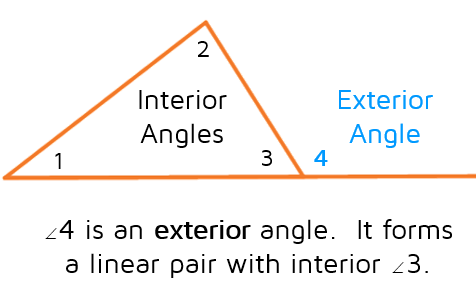
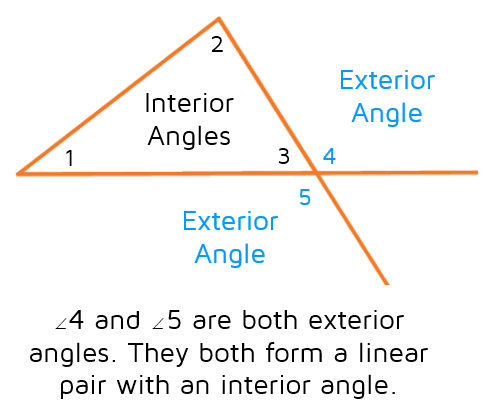
Here's a nonexample that might help. Angle 6 is on the outside of the triangle, but it is not an exterior angle. Angle 6 is a vertical angle with an interior angle, but it's not forming a linear pair with an interior angle. An exterior angle must be right next to an interior angle, the two angles have to share a side (not just a vertex).
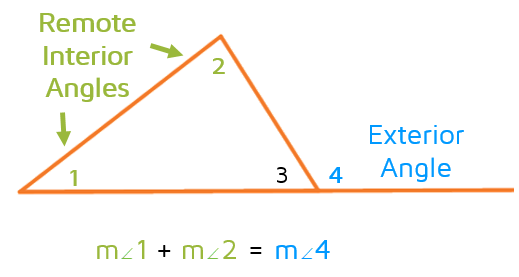
Remote Interior Angles
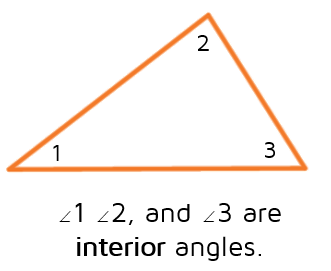
In order to understand the Exterior Angle Theorem, it's important that you know about remote interior angles. Remember, interior angles are on the inside of a triangle.
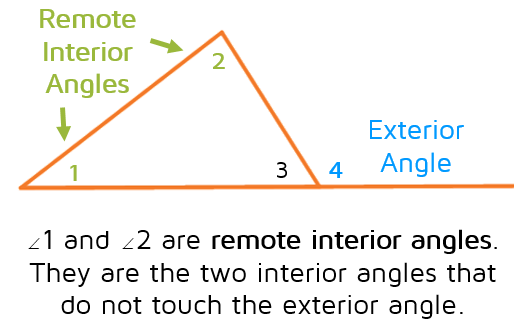
Each exterior angle has 2 remote interior angles. The remote interior angles are the two angles on the inside of the triangle that are not touching the exterior angle. Think of them as the "far away" inside angles, they are on the other side of the triangle, away from the exterior angle.
Each exterior angle has 2 remote interior angles. The remote interior angles are the two angles on the inside of the triangle that are not touching the exterior angle. Think of them as the "far away" inside angles, they are on the other side of the triangle, away from the exterior angle.
Finding the Measure of an Exterior Angle
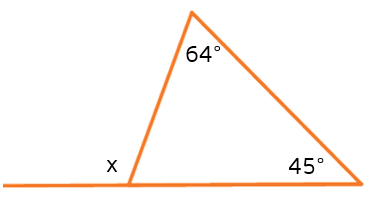
If you know the measures of the two remote interior angles, you can use them to find the measure of the exterior angle. Let's say we have the triangle below and we're trying to find x, the measure of the exterior angle.
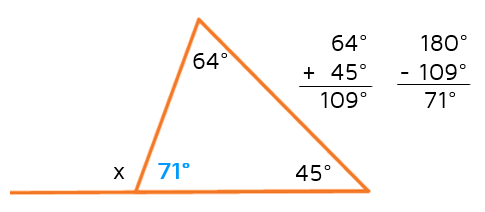
We know that the three interior angles of any triangle always add up to 180 degrees. This means we can add the 64 and 45 together and subtract that from 180 to find the missing interior angle (the one right next to the x).
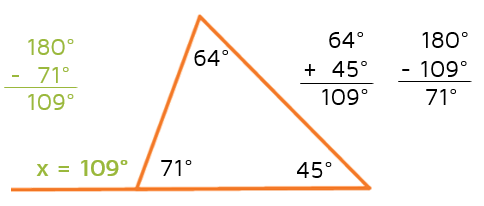
How does this help us find x? The 71 degree angle that we just found forms a linear pair with the exterior angle. This means that these two angles must add up to 180 degrees. We can subtract 71 from 180 to find the measure of the exterior angle.
This gives us 109 degrees for the exterior angle.
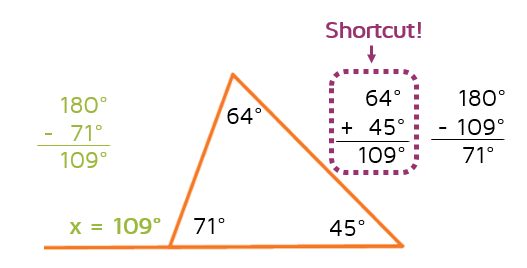
Now look back at the picture. Do you see the shortcut that we could have used to figure out that the answer was 109 degrees?
When you add the two remote interior angles together, you get the measure of the exterior angle. This shortcut has been proven to work every time and is called the Exterior Angle Theorem.
The Exterior Angle Theorem
The Exterior Angle Theorem says that if you add the measures of the two remote interior angles, you get the measure of the exterior angle. This theorem is a shortcut you can use to find an exterior angle.
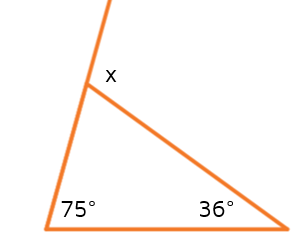
Example 1
Solve for x.
In this problem, we've been given the two remote interior angles and we need to find the exterior angles. We can use the Exterior Angle Theorem and add the two remote interior angles together to find x.
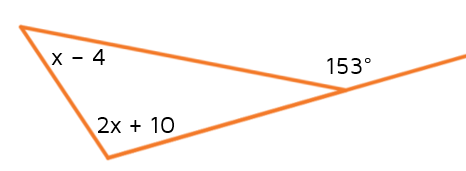
Example 2
Solve for x.
We can use the Exterior Angle Theorem to set up an equation that we will be able to solve for x. We need to add the expressions for the two remote interior angles and set it equal to the measure of the exterior angle.
Now that we have an equation set up, we can solve for x.
Practice
Ready to try a few problems on your own? Click the START button below to try a practice quiz.
|
Powered by  |